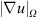Investigation of Numerical Effects on the Flow and Combustion in LES of ICE
1
Institute for Combustion and Gasdynamics, Chair for Fluid Dynamics, University of Duisburg-Essen, 47057
Duisburg - Germany
2
Center for Computational Sciences and Simulation (CCSS), University of Duisburg-Essen, 47057
Duisburg - Germany
e-mail: nguyen.thuong@uni-due.de
* Corresponding author
Received:
15
November
2016
Accepted:
30
June
2017
This work investigates the influence of numerical dissipation on the modeled combustion in Large Eddy Simulations (LES). It is well known that capturing the dynamics of the in-cylinder flow is crucial for engine simulations, as it strongly affects flame propagation. The flame propagation during the power-stroke highly depends on the turbulence level that is developed throughout compression. This turbulence level will be strongly influenced by the accuracy of the numerical schemes employed. Even a small extent of upwinding, filtering, low-order implicit time-stepping, cell-stretching or mapping between grids may affect the flow field, the turbulence level, and hence the turbulent flame speed and the pressure curve. To provide a reference, the LES in-house code PsiPhi is used, which ensures a minimum of dissipation due to high order explicit time-stepping, homogeneous and isotropic filters and cells. Good stability of the code permits the use of a second-order Central Differencing Scheme (CDS) for the transport of momentum, avoiding numerical dissipation. To analyse the effect of numerical dissipation, simulations of a fired engine are performed using different numerical schemes for the convection of momentum. Physical quantities including the total kinetic energy, the velocity gradient, the turbulent viscosity, the in-cylinder pressure, the flame propagation or the burning rate of different test cases are evaluated and compared to each other to show the numerical effects on combustion. Furthermore, the suitability of common LES quality criteria including an energy criterion and viscosity ratio is discussed based on the comparison of simulations with less and more accurate numerics. It is shown that these LES quality indicators can be highly misleading.
© T. Nguyen and A.M. Kempf, published by IFP Energies nouvelles, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
The extensive use of Computational Fluid Dynamics (CFD) in numerous engineering applications leads to many fundamental questions regarding the applied numerical approaches themselves, especially the effects of the numerical schemes on the simulation results, which have been investigated in many studies, as for examples [1-4]. Obviously, reducing the numerical errors is essential for an accurate solution of the transport equations of different physical quantities [5, 6]. It is clear that to obtain more accurate numerical results, fine grids and high order numerical schemes are preferable. However, high simulation costs due to finer computational grids as well as the numerical instability resulting from high order schemes are factors that must be considered. As a matter of fact, a compromise between accuracy, stability and convergence is often necessary. Depending on the nature of the problem, one may try and choose suitable numerical schemes that provide good results.
In order to investigate the influence of numerical schemes applied to engine simulations, several nominally 2nd-order numerical schemes are employed to examine their effect on the simulated in-cylinder flow field, as well as the combustion process. In Large Eddy Simulation (LES), investigators often outline the importance of the filter size and high-order discretization schemes to yield reasonable simulation results. However, it should be stressed that the order of numerical schemes is just one part of the story: It has been observed in many studies [6-9] that two schemes with the same nominal order of accuracy can yield very different results.
In the context of engine simulations, Misdariis et al. [10] investigated the influence of several numerical schemes for the discretization of the convective flux on the flow field and the combustion inside the engine. They observed a rather small difference between the in-cylinder flow fields resulting from the numerical schemes of second and third order of accuracy. In comparison to their findings, we observe a stronger impact of the applied numerical schemes on the small scale features of the simulation results, as illustrated in Figure 1. The Central Differencing Scheme (CDS), Quadratic Upstream Interpolation for Convective Kinematics (QUICK) and the Total Variation Diminishing (TVD) schemes yield significant differences in the velocity field where small structures are found in the whole flow field for the simulation using CDS with 2nd and 4th order, but not in the simulation with the TVD schemes. Interestingly, in spite of distinctive flow structures between different simulations, a rather small discrepancy of the total kinetic energy of the in-cylinder flow between the simulation results of all the employed schemes is achieved. This may not be overly surprising, since most of the turbulent kinetic energy exists on the larger scales. However, significant differences are observed on the smaller scales and hence the modeled sub-grid energy that has much impact on the wrinkling factor and turbulent flame speed.
 |
Figure 1 Comparison of the image-normal velocity component at −270 and −90 CAD for different numerical schemes from a chosen engine cycle. |
In the scope of this paper, the commonly used LES quality indices are also discussed. Interestingly, more dissipative schemes (like TVD) tend to cause a smaller turbulent viscosity due to smaller velocity gradients, as the numerical scheme itself is more dissipative. One may argue that with a TVD scheme, much of the dissipation is achieved by the discretization, so that the turbulence model needs to dissipate less energy. This leads to a misleading situation where many commonly used LES quality criteria must fail. Criteria based on the amount of modeled turbulent kinetic energy [11, 12], as well as the criteria based on the ratio between the turbulent and the laminar viscosity (as proposed by Celik et al. [13]), will no longer be adequate.
In this work, simulations of a four-stroke engine [14] with two intakes and two exhaust valves are performed on two different computational grids with cell sizes of 0.8 mm and 0.5 mm. To avoid the complexity of the mesh generation in a moving engine-geometry, the motion of the piston and the valves are described by Lagrangian particles in combination with an Immersed Boundary Method (IBM) [15]. This mesh-free technique has been implemented in our code PsiPhi [16] and is simple and well suited for High-Performance Computing (HPC) applications. Flame propagation is modeled using a Flame Surface Density (FSD) model [17] with iso-octane as surrogate fuel. The flow conditions at the intake and the exhaust ports of the engine are computed according to Navier-Stokes characteristic boundary conditions [18]. Our implementation [19] of Nicoud’s Sigma model [20] is used to calculate the sub-grid scale stresses.
1 Numerical Methodology for Engine Simulation
The Favre-filtered compressible Navier-Stokes equations for mass, momentum and total energy are discretized and solved numerically on an equidistant Cartesian grid using the finite-volume method. To handle the moving parts of the engine such as the piston, the intake and exhaust valves, an approach by Nguyen et al. [16] using Lagrangian particles and an IBM [15] is applied for the description of the geometries as well as the interaction between the moving boundaries and the fluid. In this approach, the moving geometries are presented with a cloud of logic and massless particles instead of the unstructured cells from body-fitted methods. The harmonic motion of the piston and the motion of the valves from the valve lift profiles are governed by the transportation of different groups of Lagrangian particles, which are used to describe the moving objects. Extensive discussion about the advantages, limitations and implementation of the method can be found in [16].
2 Combustion Modeling with Flame Surface Density
The modeling of the combustion process is described by the following equations:![$$ \begin{array}{l}\frac{\mathrm{\enspace \partial }\overline{\rho }\mathop{c}\limits^\tilde}{\mathrm{\partial }t}+\frac{\mathrm{\partial }\overline{\rho }\mathop{c}\limits^\tilde{\mathop{u}\limits^\tilde}_i}{\mathrm{\partial }{x}_i}+\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_i}\left[\overline{\rho }\left({\stackrel{\tilde }{{cu}}}_i-\mathop{c}\limits^\tilde\enspace {\mathop{u}\limits^\tilde}_i\right)\right]=\overline{\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_i}\left({\rho D}\frac{\mathrm{\partial }c}{\mathrm{\partial }{x}_i}\right)}+{\overline{\dot{w}}}_c=\overline{\rho {S}_d}{\mathrm{\Sigma }}_{\mathrm{gen}}\\ \end{array} $$](/articles/ogst/full_html/2017/04/ogst160163/ogst160163-eq1.gif) (1)
(1)
![$$ \frac{\mathrm{\partial }}{\mathrm{\partial }{x}_i}\left[\overline{\rho }\left({\stackrel{\tilde }{{cu}}}_i-\mathop{c}\limits^\tilde{\mathop{u}\limits^\tilde}_i\right)\right]=\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_i}\left(\overline{\rho }\frac{{\nu }_t}{{Sc}}\frac{\mathrm{\partial }\mathop{c}\limits^\tilde}{\mathrm{\partial }{x}_i}\right)+{F}_{\mathrm{cgt}} $$](/articles/ogst/full_html/2017/04/ogst160163/ogst160163-eq2.gif) (2)
(2)
 (3)
(3)
On the LHS of Equation (1), the sub-grid scalar flux ![$ \mathrm{\partial }/\mathrm{\partial }{x}_i[\overline{\rho }({\stackrel{\tilde }{{cu}}}_i-\mathop{c}\limits^\tilde{\mathop{u}\limits^\tilde}_i)]$](/articles/ogst/full_html/2017/04/ogst160163/ogst160163-eq4.gif) is calculated by the classical gradient hypothesis and a counter gradient term F
cgt (Eq. 2). In Equation (3), the generalized flame surface Σgen is approximated by replacing the Reynolds-averaged progress variable
is calculated by the classical gradient hypothesis and a counter gradient term F
cgt (Eq. 2). In Equation (3), the generalized flame surface Σgen is approximated by replacing the Reynolds-averaged progress variable 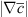 by the Favre-averaged one
by the Favre-averaged one  , where the counter gradient transport F
cgt is implicitly included (see the Discussion by Ma et al. [21]). The two terms
, where the counter gradient transport F
cgt is implicitly included (see the Discussion by Ma et al. [21]). The two terms  and D in Equation (1) are the mean reaction source term and the molecular diffusivity. In Equations (2)-(3), the turbulent viscosity, the turbulent Schmidt number, the laminar flame speed and the wrinkling factor are represented by ν
t, S
c, S
l and
and D in Equation (1) are the mean reaction source term and the molecular diffusivity. In Equations (2)-(3), the turbulent viscosity, the turbulent Schmidt number, the laminar flame speed and the wrinkling factor are represented by ν
t, S
c, S
l and 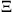 , respectively.
, respectively.
The influence of turbulence on the flame propagation is described by the wrinkling factor 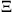 , which is modeled using an approach proposed by Muppala et al. [17].
, which is modeled using an approach proposed by Muppala et al. [17].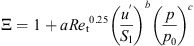 (4)
(4)
The turbulent Reynolds number Re
t is a function of the sub-grid scale velocity fluctuation u′ [22], the cell size Δ and the laminar viscosity ν: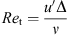 (5)
(5)
In Equation (4), the model parameters are set to b = 0.2, c = 0.2, and a = 0.46 for the iso-octane/air flame [17, 23]. In the scope of this paper, elaborated ignition modeling is not considered. Instead, we set the progress variable c to 1.0 (burned area) in a small region below the spark-plug so that the flame can start developing and propagating. It is clear that a proper ignition modeling can be done in more sophisticated ways. However, this would add additional uncertainty to the present study and be beyond the scope of the present study. We have therefore chosen to just show the effect of the numerical scheme. It is also clear that some shortcomings of numerical schemes can be partially compensated by suitable models or model constants. Further information on combustion modeling can also be found in our previous paper [16].
3 Experiment
In this study, we consider a four-stroke optical engine, which is operated by the Dreizler group at Technical University of Darmstadt [14]. The engine runs at 800 rpm with iso-octane (C8H18) as a surrogate fuel. Optical access is provided via a quartz glass cylinder liner and a flat piston window. The engine consists of a twin-cam, an overhead-valve pent-roof cylinder head with two intakes and two exhaust valves. The characteristics and operation point are shown in Table 1. For further details of the engine, the readers are referred to the paper of Baum et al. [14].
Engine specifications in the fired case.
4 Numerical Setup
The LES in-house code PsiPhi [16, 24-27] is used to solve the Favre-filtered governing equations for a compressible fluid. An equidistant Cartesian grid is used throughout the whole computational domain, which provides good accuracy and avoids the numerical dissipation caused by deformed or stretched cells of an unstructured-grid. In an equidistant Cartesian grid, the numerical error directly results from the applied interpolation scheme without adding the truncation error from the irregular grid. The disadvantage of this approach is that a local refinement is not possible, which leads to an increase of the total number of cells in the computational domain.
Results from different numerical schemes are compared: a 2nd and a 4th order CDS (CDS2, CDS4), the Limited Linear scheme [8] (LL01), the QUICK scheme [28] and two TVD schemes using CHARM [29] (TVD-CH) and Van Leer [30] (TVD-VL) limiters. It is important to note that we use a value β = 0.1 for the LL01 scheme, which makes this scheme less dissipative and supposedly “close to CDS” (Tab. 2).
The numerical schemes used in the engine simulations.
The TVD scheme with CHARM limiter [29] is used for the discretization of all scalar quantities including density  , progress-variable
, progress-variable  and total energy
and total energy  .
.
An explicit third-order Runge-Kutta scheme is employed for time integration. The unresolved turbulent viscosity is determined with Nicoud’s σ model [20] with the model constant C m of 1.5. In our experience, the combination of a sub-grid model, good equidistant Cartesian grids and an explicit low storage Runge-Kutta scheme with a small CFL number is sufficient to achieve stability – some upwinding is only introduced right at the walls and for increased Mach number. This approach has enabled stable – but not always easy to setup.
It is noted that the numerical analyses in the following sections are based on the phase-averaged data of five consecutive engine cycles for each numerical scheme. Nevertheless, we demonstrated some result from a chosen engine cycle to highlight the significant distinctions of the numerical results due to the different numerical schemes.
5 Kinetic Energy Analysis
Figure 1 shows the normal velocity components at −270 and −90 CAD, which result from six different numerical schemes. In comparison to the simulated results obtained by CDS2 and CDS4, where small structures are dominant in the flow field, much smoother flow fields are produced by the simulations using the TVD schemes (TVD-CH, TVD-VL, LL01). On the other hand, only big structures are visible for the simulations with the TVD schemes for the momentum at −90 CAD. It is noticeable that the flow structures obtained by QUICK are somewhat in between CDS and TVD. One should note that the use of non-central schemes for momentum transport in LES is a fairly recent phenomenon, which has emerged in recent years with the availability of “LES models” in robust mainstream codes like ANSYS [31], STAR-CCM+ [32] or OpenFOAM [33].
As observed in Figure 1, the simulations using CDS with 2nd and 4th order schemes resolve more small structures in the in-cylinder flow field than the other schemes. In order to quantitatively analyze the differences, we evaluate the integral of the kinetic energy,  , the integral of the velocity gradient
, the integral of the velocity gradient ![$ |\nabla u{|}_{\Omega }={\int }_{\Omega } {\left[(\mathrm{\partial }{u}_i{)}^2+(\mathrm{\partial }{u}_j{)}^2+(\mathrm{\partial }{u}_k{)}^2\right]}^{0.5}\mathrm{d}\Omega $](/articles/ogst/full_html/2017/04/ogst160163/ogst160163-eq16.gif) and the integral of turbulent viscosity
and the integral of turbulent viscosity  inside the cylinder Ω. Figure 2 shows the comparison of the integrated kinetic energy KE
Ω
, integrated velocity gradient
inside the cylinder Ω. Figure 2 shows the comparison of the integrated kinetic energy KE
Ω
, integrated velocity gradient  and integrated viscosity
and integrated viscosity 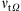 between six numerical schemes for momentum. As it is shown in Figure 2a, the total resolved kinetic energy during engine operation is quite consistent between different numerical schemes, where the maximum value of KE
Ω
is achieved around −270 CAD and gradually decreases towards the compression and expansion strokes. The spikes of KE
Ω
observed at −125 CAD and 105 CAD result from closing the intake valves and opening the exhaust valves, which cause a high velocity in the small gap between the valves and port walls. Interestingly, it is hard to notice any significant difference in the integrated kinetic energy KE
Ω
of the in-cylinder flow field between the simulations using different numerical schemes. Despite the difference in the flow structures, all the numerical schemes seem to perform very well in resolving the kinetic energy of the flow field. This may not be surprising, since most of the kinetic energy exists on the largest scales.
between six numerical schemes for momentum. As it is shown in Figure 2a, the total resolved kinetic energy during engine operation is quite consistent between different numerical schemes, where the maximum value of KE
Ω
is achieved around −270 CAD and gradually decreases towards the compression and expansion strokes. The spikes of KE
Ω
observed at −125 CAD and 105 CAD result from closing the intake valves and opening the exhaust valves, which cause a high velocity in the small gap between the valves and port walls. Interestingly, it is hard to notice any significant difference in the integrated kinetic energy KE
Ω
of the in-cylinder flow field between the simulations using different numerical schemes. Despite the difference in the flow structures, all the numerical schemes seem to perform very well in resolving the kinetic energy of the flow field. This may not be surprising, since most of the kinetic energy exists on the largest scales.
 |
Figure 2 Comparison of the integrated kinetic energy KE
Ω
, the integrated velocity gradient |
Since the wide dynamic range of data values obtained during engine simulation makes it difficult to distinguish the differences of KE
Ω
,  and
and  resulting from different numerical schemes (Fig. 2a-2c), using the normalization of all simulated data to the corresponding data obtained with the CDS2 scheme is a convenient way to highlight the variation between the schemes. As it can be seen in Figures 2a and 2d, the resolved kinetic energy yielded by the six numerical schemes using 0.5 mm grid are not significantly different from each others, whereas on the coarse grid of 0.8 mm, the resolved kinetic energy is clearly lower. As seen in Figure 2d, during the intake stroke, the total resolved kinetic energy of the simulations using more dissipative schemes such as QUICK, TVD-CH, TVD-VL and LL01 is lower than the resolved kinetic energy obtained by simulations using CDS2 and CDS4. However, during the compression stroke, KE
Ω
obtained by simulations using QUICK, TVD and LL01 seems to dissipate quite slowly in comparison to KE
Ω
obtained by CDS2 and CDS4. This may explain why we see an increasing trend of KE
Ω
from QUICK, TVD and LL01 with reference to KE
Ω
from simulations using CDS. Despite the significant differences in the flow fields obtained by different numerical schemes (Fig. 1), the resolved kinetic energy KE
Ω
of the in-cylinder flow shows no substantial difference for six studied numerical schemes. Obviously, the higher or lower value of resolved kinetic energy KE
Ω
give no definite indication whether the applied numerical scheme is more or less accurate and dissipative than other schemes. Hence, it is questionable whether the total resolved kinetic energy can be used to determine the quality of LES – or what LES quality actually is.
resulting from different numerical schemes (Fig. 2a-2c), using the normalization of all simulated data to the corresponding data obtained with the CDS2 scheme is a convenient way to highlight the variation between the schemes. As it can be seen in Figures 2a and 2d, the resolved kinetic energy yielded by the six numerical schemes using 0.5 mm grid are not significantly different from each others, whereas on the coarse grid of 0.8 mm, the resolved kinetic energy is clearly lower. As seen in Figure 2d, during the intake stroke, the total resolved kinetic energy of the simulations using more dissipative schemes such as QUICK, TVD-CH, TVD-VL and LL01 is lower than the resolved kinetic energy obtained by simulations using CDS2 and CDS4. However, during the compression stroke, KE
Ω
obtained by simulations using QUICK, TVD and LL01 seems to dissipate quite slowly in comparison to KE
Ω
obtained by CDS2 and CDS4. This may explain why we see an increasing trend of KE
Ω
from QUICK, TVD and LL01 with reference to KE
Ω
from simulations using CDS. Despite the significant differences in the flow fields obtained by different numerical schemes (Fig. 1), the resolved kinetic energy KE
Ω
of the in-cylinder flow shows no substantial difference for six studied numerical schemes. Obviously, the higher or lower value of resolved kinetic energy KE
Ω
give no definite indication whether the applied numerical scheme is more or less accurate and dissipative than other schemes. Hence, it is questionable whether the total resolved kinetic energy can be used to determine the quality of LES – or what LES quality actually is.
6 Velocity Gradient and Turbulent Viscosity
We have shown that the resolved kinetic energy may not be adequate to differentiate the influence of numerical schemes on the in-cylinder flow field, even though clear differences between these schemes are observed in Figure 1. On the other hand, the integrated velocity gradients 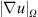 in Figures 2b and 2f show a clear distinction between numerical schemes. As expected, the
in Figures 2b and 2f show a clear distinction between numerical schemes. As expected, the 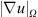 s obtained by both CDS2 and CDS4 are comparable and consistently larger than
s obtained by both CDS2 and CDS4 are comparable and consistently larger than 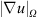 s of QUICK, TVD-CH, TVD-VL and LL01. Intuitively one may conclude that the turbulence level of the in-cylinder flow field obtained by QUICK (Fig. 1) lies somewhere in between TVD and CDS schemes. This is also clearly shown in Figures 2b and 2e where
s of QUICK, TVD-CH, TVD-VL and LL01. Intuitively one may conclude that the turbulence level of the in-cylinder flow field obtained by QUICK (Fig. 1) lies somewhere in between TVD and CDS schemes. This is also clearly shown in Figures 2b and 2e where  . Since the calculation of sub-grid turbulent viscosity
. Since the calculation of sub-grid turbulent viscosity  depends on the velocity gradient,
depends on the velocity gradient, 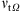 obtained by CDS2 and CDS4 are, as expected, greater than
obtained by CDS2 and CDS4 are, as expected, greater than  from QUICK, TVD-CH, TVD-VL and LL01. As shown in Figure 2f, the total sub-grid turbulent viscosity
from QUICK, TVD-CH, TVD-VL and LL01. As shown in Figure 2f, the total sub-grid turbulent viscosity  obtained from the dissipative schemes TVD-CH, TVD-VL and LL01 is just half the corresponding turbulent viscosity from CDS2 and CDS4. The distribution of the turbulent viscosity in the tumble plane in Figure 3 reveals the substantial difference between the less and more dissipative numerical schemes, where large values of the turbulent viscosity are found in the simulations using CDS2, CDS4 and QUICK. This obviously calls into question whether it is reasonable to determine good or bad LES quality based on the sub-grid turbulent viscosity, since the less dissipative numerical schemes would always lead to higher sub-grid turbulent viscosity, hence implying that more turbulence is resolved and less modeled by the more dissipative schemes.
obtained from the dissipative schemes TVD-CH, TVD-VL and LL01 is just half the corresponding turbulent viscosity from CDS2 and CDS4. The distribution of the turbulent viscosity in the tumble plane in Figure 3 reveals the substantial difference between the less and more dissipative numerical schemes, where large values of the turbulent viscosity are found in the simulations using CDS2, CDS4 and QUICK. This obviously calls into question whether it is reasonable to determine good or bad LES quality based on the sub-grid turbulent viscosity, since the less dissipative numerical schemes would always lead to higher sub-grid turbulent viscosity, hence implying that more turbulence is resolved and less modeled by the more dissipative schemes.
 |
Figure 3 Distribution of the turbulent viscosity in the tumble plane between different numerical schemes at −270 and −90 CAD from a chosen engine cycle. |
7 Turbulent Viscosity in Dissipative Schemes
To examine further the influence of sub-grid modeling in dissipative schemes such as LL01, TVD-CH and TVD-VL, a simulation without sub-grid modeling using LL01 for the discretization of the momentum is carried out. The main reason for this test is that the scheme is very popular in both LES [34, 35] and Monotone Integrated Large Eddy Simulation (MILES) [36] simulations. The numerical results obtained by two simulations with and without turbulent viscosity can be distinguished in Figure 2.
As shown in Figure 2, the differences in the resolved kinetic energy KE
Ω
of the in-cylinder flow field as well as in the absolute velocity gradient  with and without turbulent viscosity are insignificant. With LL01, the contribution of turbulent viscosity has become minimal and it is hardly noticeable. The turbulent viscosity ν
t depends on the velocity gradients which are better maintained with the CDS or QUICK schemes than with TVD or LL01 schemes. By destroying the velocity gradient, the influence of sub-grid modeling becomes negligible and the engine simulation with LL01 scheme even without using turbulent viscosity νt can still converge and produces similar results as the simulation with the LL01 scheme with a turbulent viscosity ν
t. Figure 4 demonstrates clearly the influence of sub-grid modeling on the simulations using CDS2 and LL01. This finding may imply that LES with a limited linear (or similar dissipative) scheme for momentum are actually MILES simulations (implicit LES) with an ineffectual turbulence model. In other words, such simulations might be “implicitly implicit LES”. In such cases, LES quality criteria based on the turbulent viscosity must fail.
with and without turbulent viscosity are insignificant. With LL01, the contribution of turbulent viscosity has become minimal and it is hardly noticeable. The turbulent viscosity ν
t depends on the velocity gradients which are better maintained with the CDS or QUICK schemes than with TVD or LL01 schemes. By destroying the velocity gradient, the influence of sub-grid modeling becomes negligible and the engine simulation with LL01 scheme even without using turbulent viscosity νt can still converge and produces similar results as the simulation with the LL01 scheme with a turbulent viscosity ν
t. Figure 4 demonstrates clearly the influence of sub-grid modeling on the simulations using CDS2 and LL01. This finding may imply that LES with a limited linear (or similar dissipative) scheme for momentum are actually MILES simulations (implicit LES) with an ineffectual turbulence model. In other words, such simulations might be “implicitly implicit LES”. In such cases, LES quality criteria based on the turbulent viscosity must fail.
 |
Figure 4 Image-normal velocity component at −180 CAD obtained from the simulations using CDS2 and LL01 with (left) and without (right) sub-grid modeling. |
8 How much Kinetic Energy is Contained in Small Flow Structures?
Despite the small structures are dominant in the flow field of the simulations using CDS2 and CDS4, the resolved kinetic energy obtained by these simulations is quite similar to the results obtained by TVD-CH, TVD-VL or LL01 schemes (Fig. 2a). This raises a question of how much kinetic energy is contained in small structures. In order to reasonably estimate the amount of kinetic energy containing in these small vortices, we employ a Gaussian filter with the filter size of 3Δ × 3Δ × 3Δ (Δ denotes the size of the equidistant cells) to filter the small structures out of the flow field. The coefficients of the applied Gaussian filter are presented as a 3 × 3 × 3 dimensional array:![$$ \frac{1}{64}\left(\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right],\enspace \left[\begin{array}{ccc}2& 4& 2\\ 4& 8& 4\\ 2& 4& 2\end{array}\right],\enspace \left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right]\right) $$](/articles/ogst/full_html/2017/04/ogst160163/ogst160163-eq31.gif)
The difference in kinetic energy ΔKE Ω = KEoriginal − KEfiltered between the original flow field and the filtered flow field is a good estimation of how much kinetic energy the small structures contain. Figure 5 shows the vertical velocity component and its corresponding high-pass filtered component from different numerical schemes at −180 CAD. The total kinetic energy and the difference ΔKE Ω between the original and the filtered flow field are plotted in Figure 6. According to our method, the kinetic energy contained in the small flow structures, is less than 10% of the total resolved kinetic energy of the flow field. This finding is interesting because it can explain why a comparable total kinetic energy is obtained by simulations using different numerical schemes for momentum.
 |
Figure 5 Illustration of the vertical velocity component (top) and its high pass filtered component (bottom) of different numerical schemes from a chosen engine cycle at −180 CAD using Gaussian filter of size 3Δ × 3Δ × 3Δ. |
 |
Figure 6 The difference in total kinetic energy of the original and filtered in-cylinder flow field at −180 CAD. |
From Figures 1, 2 and 6, it is clear that the dominantly small structures in the flow field, obtained by simulations using CDS, comprise just a small amount of kinetic energy in comparison to the big structures which govern the flow field of the simulations using TVD or LL schemes. In spite of holding a limited amount of kinetic energy, the fluctuations in the flow field significantly contribute to the velocity gradient and eventually, to flame propagation during combustion.
9 Dissipation Rate
The resolved dissipation rate is evaluated by the turbulent viscosity ν
t and the phase-averaged strain rate tensor 〈S
ij
〉: (6)
(6)
Figure 7 shows the distribution of dissipation rate at −180 CAD in the tumble plane. As expected, the dissipation rate obtained by the simulations with CDS2, CDS4 and QUICK exhibits much higher values in comparison to the ones achieved with TVD-CH, TVD-VL and LL01. The higher dissipation rate resulting in simulations using CDS or QUICK schemes is a quantitative indication of how well the small structures are resolved. It can be clearly seen in Figure 7 that simulations using dissipative schemes (TVD or LL01) can only resolve small structures where strong turbulence exists.
 |
Figure 7 Dissipation rate obtained at −180 CAD by simulations using different numerical schemes from a chosen engine cycle. |
The averaged dissipation rate of the in-cylinder flow for different numerical schemes is shown in Figure 8. The averaged dissipation rate from less dissipative schemes like CDS2 and CDS4 are almost two times larger the dissipation rate resulting from simulations using TVD or LL01 schemes.
 |
Figure 8 Averaged dissipation rate obtained at −180 and 0 CAD by simulations using different numerical schemes. |
10 Estimation of the Integral Length Scale
In order to estimate the integral length scale of the in-cylinder flow, one can compute the spatial correlation function (Eq. 7), in which the two-point correlation is evaluated along two chosen vertical and horizontal sampling lines (Fig. 9). We do not show the integral length-scales themselves as the number of cycles is not sufficient to determine the length-scale with sufficient precision. We show the differences in the correlation functions from which the length scales are determined instead.
 |
Figure 9 Vertical and horizontal sampling lines in the tumble plane symmetry for the evaluation of the spatial correlation function. |
The spatial correlation function R of the velocity fluctuation u′(x) reads: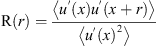 (7)
(7)
The velocity fluctuation u′(x) is calculated from the instantaneous velocity u(x) and the phase averaged velocity 〈u(x)〉: (8)
(8)
The integral length scale L is calculated by integrating R(r) along the sampling line up to the intersection point P between the curve R (Fig. 10) and the horizontal axis (s = OP): (9)
(9)
 |
Figure 10 Two-point correlation coefficients R xx and R yy of the velocity fluctuation along the vertical sampling line using the horizontal velocity fluctuation u′ (left) and the horizontal sampling line using the vertical velocity fluctuation v′ (right) of the tumble plane. |
As shown in Figure 9, the two-point correlation function is computed along two sampling lines using two velocity components: R xx is computed along the vertical line using the horizontal velocity u and vice versa. The idea is simple, a change in sign of the correlation R yy along the horizontal sampling line or R xx along the vertical sampling line can be considered as a very coarse estimation of the radius of the vortex [37]. More detailed explanation and discussion of the method can be found in the papers [12, 38].
Figure 10 shows the calculated two-point correlation function R(r) along two chosen sampling lines. To avoid confusion by plotting too much data (six schemes and 5 crank angle degrees), only results obtained from two simulations with CDS2 and TVD, are presented. Based on the Equation (9) and the comparison of the two-point coefficient curves R xx and R yy between CDS2 and TVD-VL, it would be reasonable to consider that the length scales increase with more dissipative schemes.
11 Influence of Numerical Schemes on Combustion
Figure 11 shows instantaneous volume renderings of the reaction source terms at different crank angle degrees. Since the volume rendering is quite similar between the simulations using CDS2 and CDS4 and between the simulations using TVD-CH, TVD-VL and LL01, we present only the visualization of flame propagation from simulations using CDS2, TVD-CH and QUICK instead of all six simulations. As evidenced by Figure 11, from −8 to 8 CAD, the growth rate of flame area from the CDS2 and QUICK schemes are quite comparable. The flame-wrinkling produced by these less dissipative schemes is much stronger in comparison to the wrinkling from simulations using TVD. Although the total kinetic energy produced by the six numerical schemes is obviously in agreement (Fig. 12), the obtained burning rates behave very differently. This is due to the fact, that much of turbulence is still very well “maintained” by the simulations using CDS in comparison to the ones using TVD schemes, which can be clearly demonstrated by the vertical velocity component at −16 CAD (Fig. 13). Evidently, the integrated turbulent viscosity  achieved with the simulations using CDS is more than 40% higher than the turbulent viscosity ν
t from the simulations using TVD, which directly results in a larger discrepancy in the integrated reaction source term and the in-cylinder pressure. Interestingly, the difference in
achieved with the simulations using CDS is more than 40% higher than the turbulent viscosity ν
t from the simulations using TVD, which directly results in a larger discrepancy in the integrated reaction source term and the in-cylinder pressure. Interestingly, the difference in  between the simulation using CDS and QUICK (less than 20%) does not lead to strong deviation in the flame propagation and the in-cylinder pressure, especially between the simulated results from CDS2 and QUICK up to 6 CAD.
between the simulation using CDS and QUICK (less than 20%) does not lead to strong deviation in the flame propagation and the in-cylinder pressure, especially between the simulated results from CDS2 and QUICK up to 6 CAD.
 |
Figure 11 The vertical velocity obtained by different numerical schemes from a chosen engine cycle at −16 CAD crank angle degree. |
 |
Figure 12 Volume rendering of reaction source term obtained by numerical schemes from a chosen engine cycle at different crank angle degree. |
 |
Figure 13 Comparison of the integrated kinetic energy, integrated turbulent viscosity, integrated reaction source term and in-cylinder pressure obtained for different numerical schemes. |
12 Les Quality Criteria
Determination of good or bad LES quality with a given resolution and numerical scheme has been extensively discussed in many studies [13, 38-42]. Focusing on engine simulations, some authors [12, 37] have applied several LES quality indices [11, 13]. These LES indices are used to estimate, whether a given resolution is sufficient for a “good LES”. However, most of these criteria are likely to fail due to the influence of numerical schemes on the numerical results. We have shown that simulations using highly dissipative schemes could be considered as a “good LES” since they seem to achieve less unresolved kinetic energy or less turbulent viscosity in comparison to the simulations using less dissipative schemes such as CDS2, CDS4 or QUICK. Similar arguments can also be found in the work of others [39, 43]. Obviously, any LES quality criteria, that consider the minimum of turbulent viscosity or unresolved kinetic energy as an indicator for a “good LES”, should be taken with care. To demonstrate the inadequacy of such LES quality criteria, we apply them to the LES engine simulations on the same grid using different numerical schemes.
The first criterion is the ratio of resolved turbulent kinetic energy k
res (x, t) to the amount of total turbulent kinetic energy (k
res (x, t) + k
sgs (x, t)). (10)
(10)
If a LES computation is able to resolve more than 80% of the total kinetic energy (M (x, t) > 0.8), then it is supposed to be a “good LES”. The calculations of resolved kinetic energy k
res (x, t) are outlined below.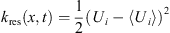 (11)where 〈U
i
〉 is the phase-averaged velocity component. The sub-grid kinetic energy k
sgs (x, t) can be modeled from the phase averaged strain rate tensor 〈S
ij
〉2 according to Equation (12) [12, 44] with the constant C
i
set to 0.202:
(11)where 〈U
i
〉 is the phase-averaged velocity component. The sub-grid kinetic energy k
sgs (x, t) can be modeled from the phase averaged strain rate tensor 〈S
ij
〉2 according to Equation (12) [12, 44] with the constant C
i
set to 0.202: (12)
(12)
Figure 14 shows the distributed value of M (x, t) as computed from the in-cylinder flow at −270, −180, −90 CAD. As discussed, six investigated schemes lead to results that satisfy the “good LES criterion” related to resolved kinetic energy. Obviously, from the PDF of M (x, t) in Figure 14, the number of points exceeding the value of 0.95 by numerical schemes like TVD and QUICK is greater than for CDS2 and CDS4. This implies that the less dissipative schemes like CDS and CDS4 resolve a smaller part of the turbulent kinetic energy in comparison to TVD, which is clearly not true.
 |
Figure 14 PDF of two LES quality indices which are evaluated for the in-cylinder flow with a bin width of 0.002. |
A second common criterion for LES quality is based on the ratio of the effective viscosity 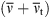 to the molecular viscosity
to the molecular viscosity  . A good LES is supposed to obtain a value of IQ
ν
above 0.8, while an IQ
ν
value of 0.952, is considered a fully resolved Direct Numerical Simulation (DNS) [13, 43].
. A good LES is supposed to obtain a value of IQ
ν
above 0.8, while an IQ
ν
value of 0.952, is considered a fully resolved Direct Numerical Simulation (DNS) [13, 43]. (13)
(13)
According to the PDF of LES IQ ν at −270, −180 and −90 CAD in Figure 14, six engine simulations with different numerical schemes satisfy the LES IQ ν index with the value of IQ ν above 0.8 for all the computational cells. Similar to the energy criterion, a larger number of computational cells from simulations using dissipative schemes such as TVD and LL01 achieves a much higher value of LES IQ ν in comparison to the LES IQ ν obtained by simulations with CDS and QUICK. Figure 15 shows the averaged values of the two LES quality criteria, in which simulations using TVD schemes always show a better “LES quality” than the simulations with CDS or QUICK schemes. As stressed in Sections 7 and 8, it is not a good approach to use a quantity, that is strongly influenced by the numerical schemes, to evaluate the quality of a simulation.
 |
Figure 15 Averaged value of LES IQ (left) and the ratio between the resolved and the total kinetic energy M (x, t) (right). |
Conclusion
This work studies the numerical effects on the flow behavior as well as the prediction of flame propagation in the context of engine simulation using LES. To carry out the investigation, six different numerical schemes (CDS2, CDS4, QUICK, TVD-CH, TVD-VL, LL) were used to discretize the momentum equation over multiple engine cycles using a real engine geometry [14].
As it was expected, small structures were found to be dominant in the flow field from simulations using less dissipative schemes (CDS2, CDS4 and QUICK), while big and smooth structures prevailed in the flow field from simulations using more dissipative schemes (TVD and LL). Interestingly, it is found that the total kinetic energy of the in-cylinder flow of all the simulations (using less or more dissipative schemes) was comparable from intake to exhaust stroke, despite much difference observed in the flow fields.
In this study, we have shown that the contribution of sub-grid modeling may be negligible for simulations using dissipative schemes such as LL or TVD. Since the velocity gradient is not well-resolved by the more dissipative schemes, the calculated turbulent viscosity is much smaller than the one obtained by simulations using less dissipative schemes.
Our study also showed that the numerical schemes have a strong effect on the combustion process since flame propagation is strongly influenced by the level of turbulence that must be well-maintained throughout the cycle. Obtaining a correct wrinkling factor or flame propagation requires a well-resolved flow field with sufficient turbulence.
We also confirm that many common LES quality criteria are inadequate to determine a “good LES”. We have illustrated that simulations using highly dissipative schemes are likely to be considered “good LES” under these criteria, which is clearly not correct.
References
- GerdesR., KöberleC., WillebrandJ. (1991) The influence of numerical advection schemes on the results of ocean general circulation models, Clim. Dyn. 5, 4, 211–226. [Google Scholar]
- NakayamaA., VengadesanS. (2002) On the influence of numerical schemes and subgrid – stress models on large eddy simulation of turbulent flow past a square cylinder, Int. J. Numer. Methods fluids 38, 3, 227–253. [CrossRef] [Google Scholar]
- EkaterinarisJ. (2005) High-order accurate, low numerical diffusion methods for aerodynamics, Prog. Aerosp. Sci. 41, 3, 192–300. [CrossRef] [Google Scholar]
- YeeH., SandhamN., DjomehriM. (1999) Low-dissipative high-order shock-capturing methods using characteristic-based filters, J. Comput. Phys. 150, 1, 199–238. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- JasakH. (1996) Error analysis and estimation for finite volume method with applications to fluid flow, Technical Report. [Google Scholar]
- KravchenkoA., MoinP. (1997) On the effect of numerical errors in large eddy simulations of turbulent flows, J. Comput. Phys. 131, 2, 310–322. [CrossRef] [Google Scholar]
- AubinJ., FletcherD., XuerebC. (2004) Modeling turbulent flow in stirred tanks with CFD: the influence of the modeling approach, turbulence model and numerical scheme, Exp. Therm. Fluid Sci. 28, 5, 431–445. [CrossRef] [Google Scholar]
- SwebyP. (1984) High resolution schemes using flux limiters for hyperbolic conservation laws, SIAM J. Numer. Anal. 21, 5, 995–1011. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- ChockD., DunkerA. (1983) A comparison of numerical methods for solving the advection equation, Atmos. Environ. (1967) 17, 1, 11–24. [CrossRef] [EDP Sciences] [Google Scholar]
- MisdariisA., RobertA., VermorelO., RichardS., PoinsotT. (2014) Numerical methods and turbulence modeling for les of piston engines: impact on flow motion and combustion, Oil Gas Sci. Technol. – Rev IFP 69, 83. [Google Scholar]
- PopeS. (2001) Turbulent flows, Cambridge University Press, Cambridge. [Google Scholar]
- di MareF., KnappsteinR., BaumannM. (2014) Application of LES-quality criteria to internal combustion engine flows, Comput. Fluids 89, 200–213. [CrossRef] [Google Scholar]
- CelikI., CehreliZ., YavuzI. (2005) Index of resolution quality for large eddy simulations, J. Fluids Eng. 127, 5, 949–958. [Google Scholar]
- BaumE., PetersonB., BöhmB., DreizlerA. (2014) On the validation of LES applied to internal combustion engine flows: Part 1: comprehensive experimental database, Flow Turbul. Combust. 92, 269–297. [Google Scholar]
- PeskinC. (1972) Flow patterns around heart valves: a numerical method, J. Comput. Phys. 10, 2, 252–271. [NASA ADS] [CrossRef] [Google Scholar]
- NguyenT., ProchF., WlokasI., KempfA. (2016) Large eddy simulation of an internal combustion engine using an efficient immersed boundary technique, Flow Turbul. Combust. 97, 191–230. [CrossRef] [Google Scholar]
- MuppalaS., AluriN., DinkelackerF., LeipertzA. (2005) Development of an algebraic reaction rate closure for the numerical calculation of turbulent premixed methane, ethylene, and propane/air flames for pressures up to 1.0 MPa, Combust. Flame 140, 4, 257–266. [Google Scholar]
- PoinsotT., LelefS. (1992) Boundary conditions for direct simulations of compressible viscous flows, J. Comput. Phys. 101, 1, 104–129. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- RiethM., ProchF., SteinO., PettitM., KempfA. (2014) Comparison of the sigma and Smagorinsky LES models for grid generated turbulence and a channel flow, Comput. Fluids 99, 172–181. [CrossRef] [Google Scholar]
- NicoudF., TodaH., CabritO., BoseS., LeeJ. (2011) Using singular values to build a subgrid-scale model for large eddy simulations, Phys. Fluids 23 8, 085106. [CrossRef] [Google Scholar]
- MaT., SteinO., ChakrabortyN., KempfA. (2013) A posteriori testing of algebraic flame surface density models for LES, Combust. Theory Model. 17, 3, 431–482. [CrossRef] [MathSciNet] [Google Scholar]
- WyngaardJ. (1992) Atmospheric turbulence, Annu. Rev. Fluid Mech. 24, 1, 205–234. [CrossRef] [Google Scholar]
- HeywoodJ. (1988) Internal combustion engine fundamentals, vol. 930, McGraw-Hill, New York. [Google Scholar]
- KempfA., GeurtsB., OefeleinJ. (2011) Error analysis of large-eddy simulation of the turbulent non-premixed sydney bluff-body flame, Combust. Flame 158, 12, 2408–2419. [CrossRef] [Google Scholar]
- NguyenT., JanasP., LucchiniT., D’ErricoG., KaiserS., KempfA. (2014) LES of flow processes in an SI engine using two approaches: Openfoam and PsiPhi, SAE Technical Paper 2014-01-1121. [Google Scholar]
- ProchF., KempfA. (2015) Modeling heat loss effects in the large eddy simulation of a model gas turbine combustor with premixed flamelet generated manifolds, Proc. Combust. Inst. 35, 3, 3337–3345. [CrossRef] [Google Scholar]
- RittlerA., ProchF., KempfA. (2015) LES of the sydney piloted spray flame series with the PFGM/ATF approach and different sub-filter models, Combust. Flame 162, 4, 1575–1598. [CrossRef] [Google Scholar]
- LeonardB. (1979) A stable and accurate convective modelling procedure based on quadratic upstream interpolation, Comput. Methods Appl. Mech. Eng. 19, 1, 59–98. [Google Scholar]
- ZhouG. (1995) Numerical simulations of physical discontinuities in single and multi-fluid flows for arbitrary Mach numbers, Chalmers University of Technology, Gothenburg, Sweden. [Google Scholar]
- Van LeerB. (1974) Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme, J. Comput. Phys. 14, 4, 361–370. [NASA ADS] [CrossRef] [Google Scholar]
- KeatingM. (2011) Accelerating CFD solutions, Advantage 1, 48. [Google Scholar]
- GrigorievM., SwiatekC., HittJ. (2010) Benchmarking CD-Adapco’s Star-CCM+ in a production design environment, ASME Turbo Expo 2010: Power for Land, Sea, and Air, June 14-18, Glasgow, UK, American Society of Mechanical Engineers, vol. 7, pp. 1019–1025. [CrossRef] [Google Scholar]
- JasakH., JemcovA., TukovicZ. (2007) Openfoam: A C++ library for complex physics simulations, in: International Workshop on Coupled Methods in Numerical Dynamics vol. 1000, IUC Dubrovnik, Croatia, pp. 1–20. [Google Scholar]
- KeskinenJ.-P (2016) Large eddy simulation of in-cylinder flows, PhD Thesis, Aalto University. [Google Scholar]
- WehrfritzA., VuorinenV., KaarioO., LarmiM. (2013) Large eddy simulation of high-velocity fuel sprays: studying mesh resolution and breakup model effects for spray a, Atomization Sprays 23, 5, 419–442. [CrossRef] [Google Scholar]
- BorisJ., GrinsteinF., OranE., KolbeR. (1992) New insights into large eddy simulation, Fluid Dyn. Res. 10, 4-6, 199–228. [NASA ADS] [CrossRef] [Google Scholar]
- JanasP., WlokasI., BöhmB., KempfA. (2017) On the evolution of the flow field in a spark ignition engine, Flow Turbul. Combust. 98, 237–264. [Google Scholar]
- BreuerS., OberlackM., PetersN. (2005) Non-isotropic length scales during the compression stroke of a motored piston engine, Flow Turbul. Combust. 74, 2, 145–167. [CrossRef] [Google Scholar]
- KleinM. (2005) An attempt to assess the quality of large eddy simulations in the context of implicit filtering, Flow Turbul. Combust. 75, 1-4, 131–147. [CrossRef] [Google Scholar]
- GousseauP., BlockenB., Van HeijstG. (2013) Quality assessment of large-eddy simulation of wind flow around a high-rise building: validation and solution verification, Comput. Fluids 79, 120–133. [CrossRef] [Google Scholar]
- FreitagM., KleinM. (2006) An improved method to assess the quality of large eddy simulations in the context of implicit filtering, J. Turbulence 7, N40. [Google Scholar]
- AddadY., GaitondeU., LaurenceD., RolfoS. (2008) Optimal unstructured meshing for large eddy simulations, in: Quality and reliability of large-eddy simulations, Springer, Dordrecht, pp. 93–103. [CrossRef] [Google Scholar]
- PettitM., CoritonB., GomezA., KempfA. (2011) Large-eddy simulation and experiments on non-premixed highly turbulent opposed jet flows, Proc. Combust. Inst. 33, 1, 1391–1399. [CrossRef] [Google Scholar]
- YoshizawaA. (1986) Statistical theory for compressible turbulent shear flows, with the application to subgrid modeling, Phys. Fluids (1958-1988) 29, 7, 2152–2164. [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Figure 1 Comparison of the image-normal velocity component at −270 and −90 CAD for different numerical schemes from a chosen engine cycle. |
| In the text | |
 |
Figure 2 Comparison of the integrated kinetic energy KE
Ω
, the integrated velocity gradient |
| In the text | |
 |
Figure 3 Distribution of the turbulent viscosity in the tumble plane between different numerical schemes at −270 and −90 CAD from a chosen engine cycle. |
| In the text | |
 |
Figure 4 Image-normal velocity component at −180 CAD obtained from the simulations using CDS2 and LL01 with (left) and without (right) sub-grid modeling. |
| In the text | |
 |
Figure 5 Illustration of the vertical velocity component (top) and its high pass filtered component (bottom) of different numerical schemes from a chosen engine cycle at −180 CAD using Gaussian filter of size 3Δ × 3Δ × 3Δ. |
| In the text | |
 |
Figure 6 The difference in total kinetic energy of the original and filtered in-cylinder flow field at −180 CAD. |
| In the text | |
 |
Figure 7 Dissipation rate obtained at −180 CAD by simulations using different numerical schemes from a chosen engine cycle. |
| In the text | |
 |
Figure 8 Averaged dissipation rate obtained at −180 and 0 CAD by simulations using different numerical schemes. |
| In the text | |
 |
Figure 9 Vertical and horizontal sampling lines in the tumble plane symmetry for the evaluation of the spatial correlation function. |
| In the text | |
 |
Figure 10 Two-point correlation coefficients R xx and R yy of the velocity fluctuation along the vertical sampling line using the horizontal velocity fluctuation u′ (left) and the horizontal sampling line using the vertical velocity fluctuation v′ (right) of the tumble plane. |
| In the text | |
 |
Figure 11 The vertical velocity obtained by different numerical schemes from a chosen engine cycle at −16 CAD crank angle degree. |
| In the text | |
 |
Figure 12 Volume rendering of reaction source term obtained by numerical schemes from a chosen engine cycle at different crank angle degree. |
| In the text | |
 |
Figure 13 Comparison of the integrated kinetic energy, integrated turbulent viscosity, integrated reaction source term and in-cylinder pressure obtained for different numerical schemes. |
| In the text | |
 |
Figure 14 PDF of two LES quality indices which are evaluated for the in-cylinder flow with a bin width of 0.002. |
| In the text | |
 |
Figure 15 Averaged value of LES IQ (left) and the ratio between the resolved and the total kinetic energy M (x, t) (right). |
| In the text | |