© P. Bérest & F. Louvet, published by IFP Energies nouvelles, 2020

1 Introduction

Salt caverns are created through solution mining (Habibi, 2019). They are connected to ground level through a 200-m to 2000-m cemented casing (see Fig. 1a). A hanging string is set in the well, like a straw in a bottle; water is injected through the hanging string in the cavern, where solution takes place; and the formed brine is removed from the cavern through the annulus between the hanging string and the cemented casing. Cavern volumes range from V₀ = 5000 m³ to 1 000 000 m³.

Fig. 1 From left to right: (a) solution mining; (b) debrining; (c) end of debrining; (d) before commissioning.

The purpose of these caverns is to provide chemical plants with brine or to provide storage capacity for liquid or gaseous hydrocarbons. Several dozens of them are used in France for natural gas storage (100 in Germany). It is generally believed that such caverns will be used in the future for storage of compressed air or hydrogen (Bérest, 2017).

When solution-mining is completed, the cavern is filled with brine. In the case of gas storage, gas then is injected in the annulus (Fig. 1b), pushing downward a brine-gas interface in the cavern (Brine is withdrawn through the hanging string.) until the interface reaches the lowest end of the central string (“debrining”), Figure 1c. The cavern bottom is filled with insoluble debris that accumulated there during leaching. The hanging string must not be stuck in the insoluble debris as it is removed from the cavern at the end of debrining (Fig. 1d). For this reason, the string end must be set slightly above the debris, and some brine unavoidably is left at the cavern bottom. This brine sump (in fact, a mixture of insoluble debris and brine) plays a significant role in the thermal and thermodynamic behavior of the gas-storage facility, as it provides gas with water vapor.

This paper discusses the thermodynamic behavior (pressure, temperature, water content) of salt caverns used for gas storage. This topic was discussed by several authors from the standpoint of numerical computations, for instance Nakhamkin et al. (1990) or Thaule (1997). In this paper, a more inductive approach is adopted: a tentative description of the main phenomena is inferred from temperature measurements performed in actual salt caverns.

During the leaching process, cold water pumped from a lake or a shallow aquifer layer at ground level is injected in the cavern (its temperature may be 10–12 °C). When debrining ends, brine left at cavern bottom is still significantly colder than the salt formation at cavern depth, which typically has a geothermal temperature of 45 °C at a depth of 1000 m. During the storage operation, gas cools (when gas is withdrawn) or warms (when gas is injected). The typical temperature of injected gas is 60 °C (40–50 °C in Storengy caverns). One can expect that bottom brine temperature slowly increases to reach thermal equilibrium with the salt formation. In fact, in the long term, the bottom brine temperature decreases as shown by Figure 2 which represents evolutions of as-measured sump brine temperature and average gas temperature in a gas storage cavern operated by Storengy. Solution mining was conducted over 6 years. When debrining was complete (Year 0), the brine temperature was 38 °C. Geothermal temperature at cavern depth is T_∞ = 55 °C. Several temperature profiles were run during Years 9–24. Although brine temperature is warmer than at the end of debrining, it remains consistently colder than the rock mass – and even decreases over time. This is unexpected. Orders of magnitude can be obtained as follows. V₀ = 270 000 m³ is the volume of the cavern; α = 3.75% is the volumetric fraction of insoluble materials (anhydrite, clay, etc.) in the salt formation; the volume of fallen blocks at the cavern bottom is αV₀; and the overall volume occupied by the blocks (including the porosity between the fallen blocks) is V_bs = αfV₀, where f is the “bulking factor”; f = 1.5 is typical. The brine sump, which contains both brine and insoluble rock blocks, has a heat capacity that is the sum of the heat capacity of brine or (f − 1) αV₀ρ_bC_b and the heat capacity of insoluble blocks or αV₀ρ_iC_i. The brine sump is assimilated to a half-sphere with a typical radius of R = 19 m (its volume is V_bs = 15 000 m³), and when ρ_bC_b = 3.8 × 10⁶ J/m³/°C and ρ_iC_i = 2 × 10⁶ J/m³/°C, its average heat capacity is ρ_bsC_bs = 2.6 × 10⁶ J/m³/°C. Heat transfer through the brine-gas interface is disregarded (This assumption will be discussed in Sect. 5.3). Heat transfer through the rock mass can be described through two equations: (1) heat conduction in the rock mass, ∂T_salt/∂t = k_salt ΔT_salt, where k_salt = 3 × 10⁻⁶ m²/s is the thermal diffusivity of salt; and (2) heat balance in the brine sump, , where K_salt is thermal conductivity of salt, and Σ_bs is the surface of the brine sump wall. These two equations provide two characteristic thermal times, t₁ = R²/k_salt and t₂ = R²ρC/K_salt, which are not very different – for instance, K_salt = 6 W/m/°C, k_salt = 3 × 10⁻⁶ m² leads to t₁ = 3.6 years and t₂ = 2.8 years. Although it should be expected that brine temperature evolution follows the trend represented by the dotted line on Figure 2 (Sump temperature rises rapidly first, then more slowly when it is closer to rock temperature, and, after 10 years, final equilibrium should be reached.) Figure 2 proves that it does not.

Fig. 2 As-observed brine sump temperature (blue dots), and average gas temperature (black dots) in a Storengy natural gas cavern. The dotted line is the computed brine sump evolution when a 2.25 year characteristic time is assumed.

Note that gas temperature is always warmer than brine-sump temperature (Figs. 2–6) even if, during storage operation, cavern gas experiences large pressure swings; when pressure drops abruptly, a severe temperature drop (several dozens of °C) is observed. For simplicity, it is assumed that gas temperature and pressure (T, P) are uniform in the cavern; and the gas is perfect, Pv = rT, e = C_vT and h = C_PT (state equation, internal energy and enthalpy, respectively). The equation for conservation of energy can be written

(1)

where m is the mass of gas in the cavern, is the heat flux transferred from the rock mass to the gas through the cavern wall, , hⁱⁿ is the enthalpy of the injected gas, is the rate of vapor condensation (discussed in Sect. 5) and L the latent heat of vapor condensation. Average gas temperature is warmer than brine-sump temperature because: (1) at rest , the second thermal characteristic time, is much shorter than in the case of the brine sump (for instance, for methane at 40 °C and 15 MPa, instead of ρ_bsC_bs = 2.6 × 10⁶ J/m³/°C for the brine sump, and t₂ = 2 days), and the gas temperature cannot remain very different from rock temperature perennially; (2) when gas temperature is colder than the brine-sump temperature at the brine-gas interface, convection appears in the lower part of the gas body and warms gas effectively (see Sect. 4 and Fig. 6); and (3) temperature of the injected gas most often is warmer than the rock temperature at cavern depth, and additional enthalpy is provided to the cavern gas, a phenomenon that has no counterpart when gas is withdrawn from the cavern. One objective of this paper is to explain why brine sump remains perennially cold.

2 Convection in a cavern at rest

2.1 Induced geothermal gradient in a fluid-filled cavern

On Figure 3, temperature distribution in the well and in the cavern, along its vertical axis of symmetry, is represented for the cases of a brine-filled cavern (Fig. 3a, after Banach and Klafki, 2009) and a gas-filled cavern operated by Storengy (Fig. 3b). In both wells, temperature profiles above the caverns reflect geothermal temperature. The temperature gradient is smaller in the salt formation ( = 18 × 10⁻³ °C/m) than in the overlying layers, as the salt thermal conductivity is larger (K_salt = 6 W/m/°C instead of K_marl = 3 W/m/°C).

Fig. 3 Temperature distribution along the axis of symmetry: (a) in a brine cavern (after Banach and Klafki, 2009); (b) in the Storengy 1 natural gas storage. (Cavern shape is drawn on the left of each picture.)

Gas or brine conductivity is much smaller than that of salt (for air, K_air = 0.026 W/m/°C; for brine, K_b = 0.6 W/m/°C – see Tab. 1), and one can expect the temperature gradient to be large when conduction is the main heat-transfer mechanism in the cavern fluid. Consider, for instance, the case of an idealized spherical cavern, radius a, whose origin is at the center of a cavern whose depth is H; spherical coordinates are used, and z = H + rcos θ is oriented downward. Let T_salt and T_F be the steady-state temperature distributions in the salt mass and in the cavern fluid, respectively. Both are harmonic functions, ΔT_salt = 0 and ΔT_F = 0. At the cavern wall, temperatures and heat flux are continuous, T_salt = T_F and K_F∂T_F/∂n = K_salt∂T_salt/∂n, from which it is inferred thatK_F is much smaller than K_salt and the induced geothermal gradient in the fluid at rest is larger than the geothermal gradient in the rock mass. For air:

In fact, in these two caverns (Fig. 3), the temperature gradient is exceedingly small, because fluids are stirred by natural convection. At the cavern bottom, the fluid is slightly warmer – and less dense – than at the cavern top; due to the buoyancy effect, warmer bottom brine rises upward and is replaced by colder brine from the cavern top, which leads to the formation of convection cells. However, a striking difference is the inversion of the temperature gradient at the bottom of a gas cavern (see Sect. 3), a feature never observed in the case of a brine cavern.

2.2 First condition for onset of natural convection: adiabatic gradient

Onset of natural convection can be explained as follows. In a fluid-filled cavern, mechanical equilibrium is reached when , where P and T are fluid pressure and temperature, respectively; ρ is fluid density; and is gravity acceleration. As a result, at equilibrium, P is a function of z only; in addition, , and T also is a function of z only – P = P(z) and T = T(z). Such equilibrium is stable when temperature decreases with depth, dT/dz < 0 (cold fluid lays below warm fluid). When cold fluid lays above warm fluid, dT/dz > 0, equilibrium is unstable provided that the temperature gradient is large enough, as is well known from the study of meteorological phenomena in the atmosphere. In fact, when a small fluid portion rises by dz < 0, its pressure immediately decreases by dP = ρgdz to reach mechanical equilibrium with its new environment. Because of this expansion, fluid temperature decreases, and heat transfer occurs in order that the temperature of the fluid portion also reaches equilibrium with its environment. However, this process is much slower than the mechanical process, especially when the portion size is not especially small. During a fast rise, fluid-portion evolution is adiabatic. (Hence, entropy is constant, as viscous forces are disregarded – see Sect. 2.3.)

2.2.1 Adiabatic gradient in a dry-gas cavern

For an ideal gas, P = ρrT, Tds = C_p dT_ad − dP/ρ = 0, where s is the gas entropy per unit of mass, and C_P is the gas thermal capacity (when gas pressure is kept constant), from which This adiabatic gradient, must be compared to the induced geothermal gradient in the cavern. When the rising particle remains warmer (and lighter) than its environment and keeps rising: convection appears when the geothermal gradient in the cavern is not too small. Gravity acceleration is g = 10 m/s²; at 30 °C and 10 MPa, heat capacity is C_P = 3000 J/kg/°C for natural gas, C_P = 1170 J/kg/°C for air and C_P = 14 500 J/kg/°C for hydrogen. In other words, as in a gas cavern (see Sect. 2.1), onset of convection is likely in a air-storage facility highly likely in a natural gas storage , and certain in a hydrogen storage Note that the adiabatic gradient is slightly different when gas is saturated with water vapor (see the next section).

2.2.2 Adiabatic gradient in a wet-gas cavern

In a quiescent cavern, gas often is saturated with water vapor when equilibrium with sump brine is reached (see Sect. 5). In principle, when computing adiabatic gas expansion, the effect of condensation must be taken into account, and the wet adiabatic gradient is smaller than the dry adiabatic gradient (Sivoukhine, 1982, pp. 499–501). Let m, μ, μ^cd be the mass of gas, water vapor and liquid water in the gas, respectively. When condensation starts, μ^cd = 0, and The vapor pressure at saturation, is a function of temperature only. During adiabatic evolution, the entropy of the mixture, is constant, and (2)

Let be the latent heat for liquid-vapor transition. Taking into account (Clapeyron’s law), (mechanical equilibrium), and (state equations), equation (2) can be rewritten as(3)

The difference between the wet adiabatic gradient, 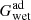, and the dry adiabatic gradient, (which equals ), is proportional to the ratio. This ratio between vapor pressure and gas pressure is not very small in the atmosphere (P_g = P_atm = 0.1 MPa); at θ = 30 °C, (30 °C) = 4.25 kPa and ) and the difference is significant when meteorological phenomena are concerned. The same is not true for a gas cavern, in which P_g = 10 MPa, and when θ = 50 °C, 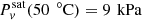and are typical.

2.2.3 Adiabatic gradient in a liquid cavern

In the case of a liquid, the state equation can write and where α is the thermal expansion coefficient of the liquid (for a gas, αT = 1). For brine, T = 300 K is typical, , and is much smaller than the induced geothermal gradient, : the onset of convection is certain in a brine-filled cavern, as suggested by the example shown on Figure 3a.

2.3 Second condition for onset of convection

In a cavity of (very) small dimensions, viscosity can impede natural convection. The set of equations describing natural convection in a cavern (conservations of mass, energy and momentum) must be solved numerically. However, steady-state convective flow can be described through linearized equations (Boussinesq approximation, Landau and Lifschitz, 1971). This set of equations highlights the significance of three dimensionless numbers, the Prandtl, Grashof and Nusselt numbers: Pr = ν/k, where ν is the fluid kinematic viscosity, k is the fluid thermal diffusivity; where a is the cavern characteristic length, and where G_c is the actual thermal gradient in the cavern; and where is the heat-transfer coefficient at the cavern wall, Natural convection starts when G is larger than the value given by a certain combination of Gr, Pr and Nu that depends on cavern shape and boundary conditions. For an elongated cylindrical cavern, convection appears when the Rayleigh number, Ra = Pr × Gr, is larger than a value that depends on Nu and is smaller than 10³ (Landau and Lifschitz, 1971). The Prandtl number can be written Pr = μC_P/K; for most gases (Tab. 1), dynamic viscosity is in the range μ = 1–2 × 10⁻⁵ Pa s, C_P = 1–2 × 10³ J/kg/K, and K = 2 × 10⁻³ W/m/K. Also, g = 10 m/s², G = 1.5 × 10⁻² °C/m, α_g = 3 × 10⁻³ °C; for standard caverns, a = 10–50 m. The Rayleigh number (Ra = Pr × Gr) is larger than 10¹⁰, a figure for which natural convection is turbulent. In other words, a cavern contains so large a fluid body that the condition relative to the adiabatic gradient is a sufficient condition for onset of convection.

2.4 Conclusion

This analysis proves that, in principle, the conditions for onset of natural convection are met in any fluid-filled cavern, whether the fluid is gas, brine or oil. However, this is not exactly true in an actual gas-filled cavern (see Sect. 3).

3 Convection in a quiescent gas cavern

On Figure 4, five vertical temperature profiles along the axis of symmetry of a cavern are represented. The same level of information is not available for the five caverns. S107 is a natural-gas cavern (V₀ = 288 000 m³) at Stassfurt, Germany (Fig. 4a). The cavern had been kept at rest for 2.5 months before the temperature log was run. As expected, the thermal gradient in the upper part of the cavern (see Tab. 2) is much smaller than the geothermal gradient in the salt formation (which is ). Slightly above the cavern bottom, the temperature-gradient sign changes (“gradient inversion”, see Tab. 2).

Fig. 4 Temperature distribution along the axis of symmetry in gas caverns: (a) S107 cavern (Klafki et al., 2003); (b) Storengy 1 natural gas cavern; (c) a cavern mentioned by Berger et al. (2002) – cavern shape is unknown; (d) a cavern mentioned by Thaule and Gentzsch (1994) – cavern shape is unknown; (e) a cavern mentioned by Krieter and Gotthardt (2015).

In the Storengy 1 cavern, the same trend is observed (Fig. 4b). Berger et al. (2002) describe a gas cavern in which the temperature gradient, in the upper part of the cavern, between 1080 m and 1300 m, is positive and small, dT_F/dz = 4 ×10⁻³ °C/m (Fig. 4c). However, between 1300 m and 1340 m (the gas-brine interface depth), the temperature gradient is negative and high: in these three caverns convection does not take place in the lower part of the cavern’s gas body, a feature also observed in Figure 4d, an example described by Thaule and Gentzsch (1994). On Figure 4e, temperature and pressure are represented (Krieter and Gotthardt, 2015). The pressure gradient increases at a 1066-m depth, the depth of the interface. A gradient temperature inversion can be observed at a approximate depth of 1025 m. In most cases, brine temperature is colder than rock temperature at sump depth, typically by 2–4 °C.

In these five caverns, a few dozen meters above the gas-brine interface, a temperature gradient inversion is observed (black arrows on Fig. 4). Such a phenomenon is observed commonly in the atmosphere above big cities and is often described as a pollution trap. Each cavern can be divided in two parts: an upper part, where convection is active (stirring both gas and water vapor); and a lower part that is the seat of thermal conduction and water vapor diffusion (and no convection). The jump in temperature gradient (and vertical heat flux) can be explained by the horizontal convective flow at inversion depth. This pattern is observed in almost all gas caverns: “… frequently, measurements in caverns reveal a drop in temperature a few meters above the brine level. This is attributable to the consumption of heat energy for evaporation” (Berger et al., 2002, p. 56); “The brine remaining in the bottom of the cavern is usually cooler than the stored gas” (Istvan, 1996, p. 3); and “Above the gas-brine level the temperature decreases significantly which is a typical effect observed in caverns” (Schneider et al., 2002, p. 263). Temperature profiles reproduced by Karimi-Jafari et al. (2014) or Osnes et al. (2007) confirm this conclusion: convection is hindered by the presence of cold brine at the cavern bottom. Remarkably, even though these caverns are of different shapes and ages, in none of them, sump brine has reached thermal equilibrium with the rock mass.

4 Convection in active caverns

In Section 3, quiescent caverns were discussed. In these caverns, the cavern gas reached thermal equilibrium, at least approximately. In fact, gas caverns are cycled between a minimum and a maximum pressure. When divided by casing-shoe depth, these pressures are converted into pressure gradients (in MPa/m), which allows for easier comparison. Minimum and maximum pressure gradients at casing-shoe depth typically to 0.018 MPa/m from 0.006 MPa/m: in a 1000-m deep cavern, gas pressure varies between 6 MPa and 18 MPa, typically. Cycle period is one year in a seasonal natural-gas storage; it is one day in a compressed air storage; however, cycle amplitude often is only a part of the maximum allowed amplitude (to 0.18 MPa/m from 0.06 MPa/m).

As was observed in the Introduction, even in a seasonal storage, gas temperature experiences significant changes during cycles. Instead of m, T (Eq. (1)) it is convenient to use P, T as main variables. Consider the case of a gas withdrawal. For short period of time (a few days) cavern wall can be considered as the sum of small flat surfaces through which heat flux per surface unit is (πk_saltt)^−1/2 when gas temperature is lowered by a temperature unit at t = 0 and kept constant. In an actual cavern, heat flux is obtained through a convolution, and, after some algebra (Bérest, 2019), conservation of energy (Eq. (1)) can be written:(4)where Σ is the overall surface of the cavern walls, and γ is the adiabaticity index; possible phase change is not considered (for natural gas or air, γ = 1.4). Heat flux from the rock mass plays a larger role for temperature evolution when the surface/volume ratio (Σ/V) is larger. (Evolution is closer to adiabatic when this ratio is smaller – i.e., in a larger cavern.)

The temperature profile along the axis of symmetry of the Storengy 2 gas cavern is represented on Figure 5. The black curve denotes the temperature profile after a gas injection. Here, again, a clear difference can be observed between the upper part of the cavern (in which the gas-temperature gradient is small and positive) and the lower part (in which it is negative), see Table 2. The grey curve is obtained after several gas movements followed by a large gas withdrawal. Temperature distribution is transient. In the chimney and casing above the cavern roof, below 1385 m, gas temperature increased, as warm gas flowing upward from the cavern circulated in the well. In the cavern itself, temperature dropped as a result of gas expansion. However, temperature drop is a function of depth, as it is lessened by heat transfer from the rock mass, which is more effective when the cavern radius is smaller, as shown above (Eq. (4)). For this reason, several slices can be sorted out according to the magnitude of the surface/volume ratio. It is likely that an individual convection cell forms in each of these slices. (A similar pattern is clearly visible in Klafki et al., 2003, Figs. 4 and 5, p. 184). Note that a small spike is visible in the temperature profile at brine-gas interface depth, a feature that appears also in Figure 4d.

Fig. 5 Gas-temperature profile along the axis of symmetry in the Storengy 2 cavern: (right) after gas injection (black) and after gas withdrawal (grey) and (left) cavern shape.

New features appear in Figure 6. More than 7 years after debrining (the cavern is relatively old), temperature profiles were measured in a cavern operated by Enterprise in Texas (Skaug et al., 2010) before and after gas withdrawal. The cavern volume is V₀ = 430 000 m³, and its depth is between H = 1100 m (3600 ft) and 1205 m (3950 ft). Cavern shape is unknown. Gas pressure (computed at 1144-m depth) was decreased from 18.8 MPa to 13.7 MPa (from 0.0164 MPa/m to 0.0117 MPa/m) between April 2009 and May 2009. Here again, before withdrawal, brine is colder than gas and rock temperature, and a temperature gradient inversion is observed at a depth of 1135-m (3720-ft). During withdrawal, gas temperature drops and becomes colder than brine temperature in the lower part of the cavern, where convection appears, leading to an almost vertical gas temperature profile, from 1170 m (3840 ft) to 1205 m (3950 ft).

Fig. 6 Enterprise Cavern 1 Temperature evolution (after Skaug et al., 2010).

5 Water vapor

5.1 Moisture content in an gas cavern

Moisture content (i.e., water vapor content) is a critical issue when operating a gas cavern. In fact, natural gas injected in a cavern is relatively dry. In France, for instance, water vapor concentration in a mass of gas injected in a cavern must be less than , where μⁱⁿ is the mass of vapor contained in a mass of injected gas whose “normal” (standard) volume is (in Nm³); P_v and P_g are the partial pressures of vapor and gas respectively; for water vapor, r_v = 460 J/kg/°C, the subscript N is for normal conditions, P_N = 0.10325 MPa, and T_N = 273 K; 1 Nm³ = 0.72 kg; Louvet et al., 2018.] However, there is a thin brine layer at the cavern wall (70 cm³/m², see Köckritz and Walden, 1994) and a (much larger) amount of brine in the sump at the cavern bottom, as mentioned in Section 1 and Figure 1. Equilibrium requires, at least in principle, that cavern gas is saturated with water vapor. When gas is saturated with water vapor, the partial pressure of the vapor is a function of temperature only, For instance, in the case of an air cavern, Rankine’s formula predicts A = 13.7, B = 5120 K, with T in K and T < 373 K; for pure water, ; and for saturated brine, according to Raoult’s law.

5.2 Effects of pressure cycles on moisture content in an air cavern

Following air injection or withdrawal, both the vapor mass and the air temperature in the cavern change. Consider for instance an air withdrawal. At t = 0, equilibrium was reached; air pressure, temperature and mass were P₀, T₀ and , respectively; vapor pressure (at saturation, as equilibrium was reached) and vapor mass were and respectively. After withdrawal, the same quantities are P, T, m, P_v and μ, respectively. The effect of withdrawal is two-fold. On one hand, vapor is withdrawn from the cavern; when the air-vapor mixture in the cavern is homogeneous, Assume first that no phase change occurs in the cavern, (Kinetics of vaporization-condensation is discussed in Sect. 5.4.) and vapor partial pressure becomes . On the other hand, as gas temperature decreases, vapor pressure at saturation becomes . During air withdrawal, water vapor is undersaturated or oversaturated, depending on the sign of:(5)

When withdrawal is exceedingly slow, temperature keeps constant, T = T₀ and vaporization takes place. When withdrawal is exceedingly fast, air evolution is isentropic, when Rankine’s formula is accepted, vapor mass at saturation decreases by and, at the beginning of the process, air is over-saturated with vapor and condensation takes place. In other words, the nature of the phase change in the cavern depends on how fast the withdrawal is.

In an actual cavern, condensation is more likely to occur as, most often, gas withdrawals are fast. It is reasonable to assume that condensation is spread in the whole cavern, as condensation germs (tiny salt grains) are present there. The latent heat generated by condensation of is Lδμ^cd where L is the latent heat of water vaporization; it is provided evenly to the entire air mass, whose temperature drop due to expansion (T − T₀) < 0 is somewhat lessened by the effect of condensation,

At the end of the withdrawal phase, the air warms to return to thermal equilibrium with the rock mass, warm dry air is injected in the cavern, and pressure and temperature increase to P₀ and T₀, respectively. Temperature increase leads to vaporization. In sharp contrast with condensation, vaporization takes place at the vicinity of the brine-air interface, where water is available, rather than in the whole cavern gas; latent heat now is provided by gas and brine at the vicinity of the interface (rather than by the entire air mass). Brine temperature at interface depth is colder than brine temperature in the sump: thermal convection takes place in the brine (There is no convection in the air above the interface, except when the pressure drop is quite large, see Fig. 6.). Most of the latent heat needed to vaporize water is provided by the brine sump, which is cooled by δθ^vap= Lδμ^vap/ρ_bsC_bsV_bs. A frequently operated gas cavern is a “cooling device”: at the end of a cycle, brine sump is colder than it was at the beginning.

To be more specific, a relation between P(t) and T(t) must be used. For instance, air is withdrawn from the cavern during a short (a few days) interval of time δt. Equation (4) can be approximated as: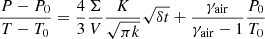(6)where and γ_air = 1.4, typically. Consider for instance a V₀ = 266 000 m³ elongated cylindrical cavern, height 536 m, radius R = 12.6 m (such figures are typical of Gulf Coast caverns) from which Brine sump volume is V_bs = 1000 m³; it contains 400 m³ (4.8 × 10⁵ kg) of brine. Pressure drops from P₀ = 10 MPa to P = 4 MPa; initial air temperature is 50 °C (323 K). From equation (6), it can be inferred that T = 303 K. Saturated vapor pressure drops from to . Air mass, which was m₀ = 3.43 × 10⁷ kg, drops to m = 1.47 × 10⁷ kg (r_air = 240 J/kg/K). Saturated vapor mass, which was , decreases to (r_v = 460 J/kg/K). After air withdrawal, actual vapor mass is air is oversaturated with water vapor and it “hazes” – or even “rains” – in the cavern. The mass of water vapor in air must decrease by 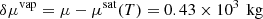and air temperature increases by (L = 2.5 × 10⁶ J/kg and were selected.) After gas injection, when equilibrium is restored, brine sump temperature decreases by was selected). Note that the maximum mass of water carried by the air withdrawn from the cavern is small when compared to the mass of brine contained in the sump, which is 4.8 × 10⁵ kg, and even frequent cycles are not able to dry up the brine sump.

5.3 Long-term evolution of brine-sump temperature

The brine sump exchanges heat through conduction (with the rock mass) and through evaporation (at the brine-gas interface)(7)where is the vapor mass rate. It can be assumed that, after some time, a type of equilibrium is reached in which the brine temperature (T_eq) is such that the average heat flux from the rock mass exactly balances the average heat amount withdrawn through vaporization. Consider, as in Section 2, a hemispherical brine sump, ; rock temperature at sump depth is , and heat flux from the rock mass is The number of cycles during one year is n, and the latent heat generated by vaporization is (in J/yr), ; n = 20/yr is assumed, from which it can be inferred that, typically, . This model has many flaws: in particular, it is far from being certain that, when the number of yearly cycles (from 10 MPa to 4 MPa and back) is high, enough time is given for vapor saturation to be completed during each cycle (see Sect. 5.4); however, it is satisfying that the computed gap between sump temperature and rock temperature is of the same order of magnitude as that observed in actual caverns (see Sect. 3). The model predicts that sump cooling is larger when cycles are more frequent.

In this model, heat flux through the gas-brine interface is typical values of dT_g/dz were provided in Table 2; this flux is negligible, as suggested in Section 1.

For instance, Quast (1983) observed that, in the early ages of the Huntorf Compressed Air Energy Storage (CAES) operation, the brine sump was cold. (There was no convection in the cavern, a negative temperature gradient was measured, and hygrometry in the cavern and in the withdrawn gas remained low.) This might be related to frequent (daily) pressure cycles in the cavern; however, in this young cavern, there are several other reasons which may explain the low temperature of the brine sump. More recent temperature profiles would have shed some light on this; unfortunately, they are not available.

A cycled cavern (gas injection followed by standstill, gas withdrawal and standstill) is a device whose effects are two-fold: (1) it pumps water from the brine-filled sump to deliver it at ground level in the withdrawn gas (Unfortunately, this process is not able to dry up the cavern, even after several decades; see Quast, 1983); and (2) it cools the brine sump, as condensation heat is provided to the entire gas body, and vaporization heat is withdrawn from the sump brine only. This explains why, in a cycled cavern, sump brine remains perennially cooler than the surrounding rock mass.

5.4 Kinetics of saturation with water vapor

It was assumed that saturation for the temperature conditions reigning in the cavern was reached immediately after (not during) any pressure change; in fact, some delay can be expected; for this reason, the actual “brine cooling device” is likely to be less effective than described in Section 5.3.

Vapor condensation following gas withdrawal is spread evenly in the whole gas mass, which is stirred by convection: rapid homogenization of vapor content is likely. A simple equation can be accepted for vapor content condensation, where the characteristic time for condensation is short, t^cd = 1 h, for instance.

In sharp contrast, following gas injection, vaporization takes place at the gas-brine interface. In the upper zone, where convection is active, water vapor is transported by gas, and its concentration tends to homogenize rapidly. However, the upper zone does not communicate directly with the brine sump, and water generated at brine-gas interface must be transferred to the upper zone through the lower zone. In the lower zone, where no convection takes place, water vapor is transported by diffusion, a much slower process, an idea already mentioned by Berger et al. (2002), and saturation is not reached immediately. For instance, Köckritz and Walden (1994) and Köckritz et al. (1996) studied (at the laboratory scale) the evaporation rate at the brine-gas interface in a closed box and proposed the following empirical law: where – i.e., , where A is the brine-gas interface area, V is the box volume and is a constant. The time constant for the vaporization process is . The ratio between cavern volume (V₀) and interface area (A) in an elongated cylindrical cavern typically is V/A = 200 m. Köckritz et al. (1996) measured (at the laboratory); they suggest that this figure must be increased by a factor of 20 when convection is active, leading to t^vap = 45 days (no convection) and t^vap = 2 days (convection active). This estimate, based on a mock-up test, does not take into account the detail of the phenomena described in this paper and must be considered as tentative. It confirms, however, that water content in the cavern gas, hence hydrate formation (see below), are related strongly to the evolution, both in space and time, of the boundary between the convective and non-convective zones. This boundary depends on many factors, including cavern shape, gas temperature history, cavern age, etc. and the equations provided in this section are simplistic.

6 Conclusion

Field data gathered in this paper suggest that, in the cavern, thermodynamic behavior of cavern gas (its temperature, pressure and water content) is governed by several coupled phenomena. During pressure cycles, temperature evolution is dictated by gas expansion-contraction and heat exchange with the rock mass; in addition, water vapor condenses in the whole gas body and evaporates at the brine-gas interface at the cavern bottom, an asymmetrical process leading to cooling of the brine sump, which remains perennially cooler than the rock mass, especially when cycles are frequent. The geothermal gradient generates natural convection in the upper part of the cavern; natural convection is impeded in the lower part of the cavern, above the brine sump, creating a buffer for water vapor diffusion in the cavern. These phenomena are important when purity of the withdrawn gas is required.

Vapor content in the cavern is an important parameter during operation of a gas cavern. When natural gas is withdrawn from the cavern, its pressure and temperature are smaller at ground level than in the cavern. When water content is high at cavern top, there is a risk that gas hydrates form at ground level. Hydrates are a significant hazard for pipes and pumps at ground level (Réveillère et al., 2016). Gas must be dehydrated before being re-injected in the grid, a costly part of storage operation. When hydrogen is stored in the cavern to be used for mobility (cars, trucks or trains), a high degree of purity is needed. Further researches are needed aiming at a better understanding of vapor distribution in a gas cavern. Qualitative explanations are provided in the paper; more quantitative results could be obtained through numerical computations.

Acknowledgments

This study was funded in part by Geodenergy, a French agency, in support of the Stopil H₂ project, devoted to hydrogen storage in salt caverns. This project includes researchers from Air Liquide, Armines, BRGM, Brouard Consulting, Ecole Polytechnique, Geostock, Ineris, Geogreen and Storengy. Andreas Bannach, Fritz Crotogino, Andreas Reitze and Nils Skaug kindly authorized reproductions in this paper of figures published in earlier reports. Thanks are given to Storengy France for accepting reproduction of high-quality field data. The authors are grateful to the Reviewers for their helpful comments. Special thanks to Kathy Sikora.

References

All Tables

All Figures

	Fig. 1 From left to right: (a) solution mining; (b) debrining; (c) end of debrining; (d) before commissioning.
In the text

	Fig. 2 As-observed brine sump temperature (blue dots), and average gas temperature (black dots) in a Storengy natural gas cavern. The dotted line is the computed brine sump evolution when a 2.25 year characteristic time is assumed.
In the text

	Fig. 3 Temperature distribution along the axis of symmetry: (a) in a brine cavern (after Banach and Klafki, 2009); (b) in the Storengy 1 natural gas storage. (Cavern shape is drawn on the left of each picture.)
In the text

	Fig. 4 Temperature distribution along the axis of symmetry in gas caverns: (a) S107 cavern (Klafki et al., 2003); (b) Storengy 1 natural gas cavern; (c) a cavern mentioned by Berger et al. (2002) – cavern shape is unknown; (d) a cavern mentioned by Thaule and Gentzsch (1994) – cavern shape is unknown; (e) a cavern mentioned by Krieter and Gotthardt (2015).
In the text

	Fig. 5 Gas-temperature profile along the axis of symmetry in the Storengy 2 cavern: (right) after gas injection (black) and after gas withdrawal (grey) and (left) cavern shape.
In the text

	Fig. 6 Enterprise Cavern 1 Temperature evolution (after Skaug et al., 2010).
In the text