Study of Gas Liquid Mass Transfer in a Grid Stirred Tank
Étude du transfert de masse gas-liquide dans une cuve agitée par grille oscillante
LMFA, UMR CNRS 5509, École Centrale de Lyon, Université Claude Bernard Lyon I, INSA de Lyon, 36 avenue Guy de Collongue, 69134
Écully Cedex – France
mahmoud.elhajem@insa-lyon.fr
* Corresponding author
Received:
6
October
2016
Accepted:
9
January
2017
Dissolution and mass transfer at gas liquid interfaces are central to many industrial and environmental issues. All these applications aim at predicting the transfer velocities between the two phases, and the dependency of these velocities on several factors such as pressure, temperature, flow regime and so on. The goal of the present study is to understand the physical phenomena acting in the liquid phase during the dissolution and transfer of a gas at a flat two-phase interface; and to measure the influence of these phenomena on mass exchanges. To that end, an oscillating grid apparatus is used to generate a controlled liquid side turbulence. The dissolution of an atmospheric sparingly soluble gas, carbon dioxide, is considered. Optical measurement techniques are used simultaneously in order to gain further insight on the hydrodynamics influence on dissolved gas mixing. The phenomena responsible for mass transfer acceleration are found to happen in thin characteristic depth scales under the interface. In those regions, a complex combination of dissolved gas injection and diffusion layers renewing events is observed. The analysis of velocity fields highlights their strongly three dimensional aspects, and simultaneous measurements, lead to the conclusion that these three-dimensional effects have an impact on dissolved scalar concentration structures, and consequently on mass transfer.
Résumé
La dissolution et le transfert de masse au niveau des interfaces gaz-liquide sont au cœur de nombreuses problématiques tant industrielles qu’environnementales. Toutes ces applications nécessitent de prédire les vitesses d’échanges de matière entre les deux phases, et la dépendance de ces vitesses d’échanges aux différentes conditions de température, pression, écoulement, etc. L’objectif de la présente étude est de comprendre les phénomènes physiques intervenant en phase liquide lors de la dissolution et du transfert d’un gaz au niveau d’une interface diphasique plane, et de quantifier l’influence de ces phénomènes sur les échanges de masse. Pour ce faire, un dispositif de grille oscillante permettant de générer une turbulence contrôlée coté liquide est utilisé. La dissolution d’un gaz atmosphérique faiblement soluble dans l’eau, à savoir le dioxyde de carbone, est considérée. Des techniques de diagnostic optique faiblement intrusives sont employées de manière simultanée pour pouvoir étudier directement l’influence de l’hydrodynamique sur le mélange du gaz. Il est observé que l’essentiel des phénomènes déterminant la vitesse de transfert de masse a lieu dans des sous-couches caractéristiques de très faible épaisseur sous l’interface. Dans ces régions, un ensemble complexe d’évènements d’injection de gaz dissout et de renouvellement des zones de diffusion est observé. L’analyse des champs de vitesse met en évidence leur caractère fortement tridimensionnel et les mesures couplées permettent de constater que ces effets tridimensionnels ont un impact sur les structures de scalaire dissout observées, et donc sur le transfert de masse.
© T. Lacassagne et al., published by IFP Energies nouvelles, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Nomenclature
R : Ideal gas constant (J K−1 mol−1)
 :
Instantaneous concentration (mol m−3)
:
Instantaneous concentration (mol m−3)
 :
Average concentration (mol m−3)
:
Average concentration (mol m−3)
c′: Fluctuation concentration (mol m−3)
 :
Instantaneous velocity field (m s−1)
:
Instantaneous velocity field (m s−1)
 :
Average velocity field (m s−1)
:
Average velocity field (m s−1)
u′ = (ux′, uy′, uz′): Fluctuating velocity field (m s−1)
j = (jx, jy, jz): Mass flux (mol m−2 s−1)
D : Diffusion coefficient (m2 s−1)
∇C : Concentration gradient (mol m−4)
 :
Turbulent mass flux (mol m−2 s−1)
:
Turbulent mass flux (mol m−2 s−1)
KL: Mass transfer coefficient (m s−1)
kL: Liquid side mass transfer coefficient (m s−1)
kg: Gas side mass transfer coefficient (m s−1)
Hc: Henry’s constant (mol m−3 Pa−1)
Csat: Scalar saturation concentration (mol L−1)
Cb: Scalar bulk/initial concentration (mol L−1)
δD: Apparent scalar sub-layer (m)
δOD: Outer diffusive sub-layer (m)
δ∞: Surface-influenced layer (m)
ν : Kinematic viscosity (m2 s−1)
T : Characteristic renewal time (s)
r : Stochastic renewal rate (s−1)
L∞: Undisturbed integral lengthscale (m)
η : Kolmogorov lengthscale (m)
ε : Turbulent dissipation rate (m2 s−3)
f : Oscillating grid frequency (Hz)
zg, H : Distances from the grid (m)
Introduction
The study of mass transfer at the interface between a gas and a liquid is of great interest in many environmental phenomena and industrial processes. In the industry, the physics of mass transfer defines the efficiency of diphasic mixing and degassing in stirred tanks, bubble columns, or even more complex mixing tank geometries.
As an example, in photobioreactors for micro-alga production, gaseous carbon dioxide CO2 has to be dissolved into the culture waters to be then consumed through photosynthesis. Optimizing micro-alga production requires a better understanding and modelling of this CO2 dissolution so that the mass transfer rate from gaseous to aqueous phase could be predicted and maximized [1].
From an environmental point of view, the same mechanisms also control the dissolution of atmospheric gases into the oceans, rivers and lakes, and have therefore a huge impact on climate and biodiversity.
Even though this issue has already been studied for several decades, its understanding is still not good enough to create realistic models suitable for implementation in Multiphase Computational Fluid Dynamics (MCFD) codes. The complexity in depicting such phenomena lies in the fact that they depend on numerous factors, among which:
-
the transported species’ Schmidt numbers in each phase
 and
and  [2];
[2]; -
the shape and dynamics of the interface [3];
-
the turbulence characteristics (intensity, size of structures, time scales, …) in each phase1.
Several investigations have been made using numerical simulations, channel flows, or stirred tank experiments to study the influence of these parameters [3-13].
All studies involving large Reynolds numbers on the liquid-side with respect to the one on the gas side agree on the fact that the influence of the interface on liquid-side turbulence is significant at very small depth in the order of 1 to 10 cm (depending on the turbulence characteristics). For high Schmidt number gases, the noticeable scalar transport events happen at even smaller depths, between around 50 μm and 200 μm.
The focus of the present study is made on the dissolution and mixing of carbon dioxide into water, with a gaseous phase at rest and a liquid phase agitated by a bottom-shear turbulence (see Fig. 1). This turbulence is generated by an oscillating grid apparatus (see Sect. 1). It is assumed that water’s flow characteristics are such that the interface remains flat. The observation area is a rectangle of about 2 cm width and 1.5 cm height underneath the surface, that is to say a “zoom inside” the surface influenced region, in a will to resolve at best the scalar sub-layers. Here, the results are given for one single set of stirring parameters, corresponding to a given Reynolds number of the flow as defined in Section 1.
 |
Figure 1 Principle of the experimental study. |
1 Background
1.1 Diffusion and Advection
In any mass transfer study, molecular diffusion is always the ultimate mechanism achieving mixing. Its expression is given by Fick’s law: (1)
(1)
With D the molecular diffusion coefficient and C the scalar field. The concentration transport equation can be written at any point as: (2)
(2)
With U the three dimensional velocity field.
Applying a Reynolds decomposition to concentration and velocity field, and averaging Equation (2), it comes (3)
(3)
The terms  ,
,  ,
,  are called turbulent mass fluxes. They are reachable only through spatially and temporally synchronised concentration and velocity measurements [14, 15], which is precisely the aim of this study.
are called turbulent mass fluxes. They are reachable only through spatially and temporally synchronised concentration and velocity measurements [14, 15], which is precisely the aim of this study.
In most of the mass transfer studies with a vertical normal interface, the mass flux is assumed to be unidirectional and Equation (3) becomes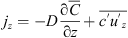 (4)
(4)
Under this assumption, mass transfer is often expressed in terms of mass transfer velocity KL defined by (5)
(5)
Lewis and Whitman [2] show that this mass transfer coefficient may be decomposed as a series association of two mass transfer velocities, one on the liquid side kL and one on the gas side kg: (6)
(6)
With R = 9.314 J K−1 mol−1 the ideal gas constant and Tg the gas temperature. For poorly soluble gases such as oxygen, nitrogen, or in this case carbon dioxide, Henry’s law constant Hc is equal to 3.3 × 10−4 mol m−3 Pa−1 and kg ≫ kL. This implies that  hence the liquid side resistance is weak and that KL ~ kL. Moreover for carbon dioxide, the diffusion coefficient in water is about
hence the liquid side resistance is weak and that KL ~ kL. Moreover for carbon dioxide, the diffusion coefficient in water is about  against
against  in air. These two properties show that the liquid side resistance to mass transfer and therefore the hydrodynamics of the liquid phase dominate mass transfers, which is why it is necessary to understand turbulence effects in the liquid phase.
in air. These two properties show that the liquid side resistance to mass transfer and therefore the hydrodynamics of the liquid phase dominate mass transfers, which is why it is necessary to understand turbulence effects in the liquid phase.
1.2 Mass Transfer Models
In order to predict mass transfer velocities/coefficients based on hydrodynamics of this liquid phase, several 1D models have been developed throughout history. What follows consist in a non-exhaustive brief review of the milestones models necessary to understand the concepts of mass transfer under the interface. Further details are provided by literature review in Herlina’s work [16].
Historically, the first assumption made was that turbulent structures could not penetrate the diffusion layer [2] and that two distinct regions could be distinguished: a pure diffusion sublayer of depth δD, and a turbulent mixing region beneath this sub-layer. The mass transfer coefficient KL can thus be expressed by Lewis and Whitman’s film model (Fig. 2) as (7)where δD may be written as
(7)where δD may be written as (8)
(8)
Further studies introduced the idea that turbulent eddies could break inside this diffusion layer and replace it with “fresh”, accelerating mass transfer in doing so. This gave birth to Higbie’s “film penetration” model [17] (9)where T corresponds to a characteristic “renewal time” that would correspond to a typical turbulent eddy turnover time-scale.
(9)where T corresponds to a characteristic “renewal time” that would correspond to a typical turbulent eddy turnover time-scale.
This model was upgraded by Danckwerts [18] by including a stochastic surface renewal rate r instead of the constant time-scale T. This is called the surface renewal model: (10)
(10)
To that point, the fact that turbulence interacts with the diffusion layer was well established. Yet, the eddies were still assumed too large to deform this layer, and only a full or partial renewal was assumed possible.
Following studies focused on including the turbulence characteristics inside what could be called “hydrodynamic models”, in comparison to the first conceptual models based on conceptual parameters to be measured or estimated. Ideas still diverged though on which of large eddies or small eddies contributed the most to mass transfer. This was expressed by the competition between the following models:
1. Fortescue and Pearson’s Large Eddy Model (LEM) [19] (11)where
(11)where  and L are characteristic velocity scale and integral large-scale of turbulence. This leads to a Re−1/2 dependency for KL.
and L are characteristic velocity scale and integral large-scale of turbulence. This leads to a Re−1/2 dependency for KL.
2. Banerjee et al. or Lamont and Scott’s [20, 21] Small Eddy Model (SEM)![$$ {K}_{\mathrm{L}}\sim \sqrt{D}{\left[\frac{\epsilon }{\nu }\right]}^{1/4} $$](/articles/ogst/full_html/2017/01/ogst160138/ogst160138-eq29.gif) (12)where ε is the turbulence dissipation rate, which gives a Re−1/4 dependency for KL.
(12)where ε is the turbulence dissipation rate, which gives a Re−1/4 dependency for KL.
Theofanous [22] reconciled these theories by showing that LEM behaviour is dominant for low Reynolds number and SEM behaviour for high Reynolds number, and proposed: (13)
(13)
More recent studies tend to confirm this double behaviour, but also present new interesting points that could lead to a better understanding of the physical phenomena.
A new range of models called Surface Divergence Models (SDM) based on the works of McCready et al. [23], Brumley and Jirka [24], Chu and Jirka [25], Hasegawa and Kasagi [9], Turney and Banerjee [3], and Banerjee et al. [26] show that the global and local mass transfer coefficients may be linked with the surface divergence β, that is to say the horizontal divergence of the velocity field at the air water interface. The generic expression of these models is (14)
(14)
The main benefit of such models is that they allow to account for surface deformations. Since it is not in the scope of this study, they will not be detailed here.
Back to vertical phenomenon considerations, it has been observed by Herlina and Jirka [5, 8] and Janzen et al. [10], and confirmed by Variano and Cowen [6, 12] that surface renewal is not the only mechanism responsible for turbulent mass transfer.
Contrary to what was previously assumed by Danckwerts [18], turbulent structures can indeed deform the diffusion layer and tend to “peel” high concentration patches and bring them down to the bulk fluid where they can be quickly mixed. This smaller scale convection like phenomena, also called “injection” events, were found to be not only observable [10, 16] but also quantitatively non negligible in the total mass flux exchanged [12]. Mass transfer seems therefore to be enhanced by a combination of injection and renewal events at different scales.
1.3 Subsurface Hydrodynamics
The previous conclusions on mass transfer lead to interrogations on the characteristics of turbulence and the induced effects close to the interface.
The first observation that can be made is that the presence of the interface tends to deform the upcoming turbulent structures by reducing their vertical dimension and increasing their horizontal scales [10, 12], as schemed on Figure 1. This implies that the bulk turbulence is different from the one impinging on the diffusion layers at the interface. A better description of this sub-surface turbulence is therefore needed.
Indeed, the model of Hunt and Graham for a turbulence near a solid surface [27], traditionally used to estimate interfacial turbulence in the mass transfer studies [24] is no longer valid for air water interface, at least when it comes to horizontal velocity fluctuations, as shown in Figure 5 of Janzen et al.’s work [10]. This figure shows that Hunt and Graham’s so called blocking theory lead to a good approximation of the behaviour of the rms of vertical velocity fluctuations near the interface. Yet, the measured profiles of RMS of horizontal velocity fluctuations do not correspond to the theory’s prediction: Hunt and Graham predict that the maximum of this RMS is at the interface whereas measurements by Janzen et al. [10] and Magnaudet and Calmet [28] show a peak at a depth of a few hundred micrometers beneath the interface.
According to Brumley and Jirka [24] from passive scalar turbulent fluctuating energy spectrum analogy, it is possible to define a priori several characteristic sub-layers sketched in Figure 3:
-
surface-influenced layer: It is the area in which turbulence characteristics are modified by the presence of the interface, of depth equal to the undisturbed integral length scale of turbulence. That corresponds to the region where large eddies begin to “see” the interface;
-
viscous sub-layer: It is the region where the viscous forces are supposed to be dominant;
-
kolmogorov sub-layer: By analogy with the surface-influenced layer, this is the depth at which the small eddies “see” the interface and are supposed to start deforming, hence the vertical velocity fluctuations are supposed to decrease linearly there.
 |
Figure 3 Characteristics sub-layers according to Brumley and Jirka [24] extracted from Herlina [16]. η is the Kolmogorov length-scale of turbulence, Sc the Schmidt number, and L∞ and ReT the integral length-scale and Reynolds number defined in Section 2.1. |
 |
Figure 4 Experimental set-up: a) side view, b) top view. |
Based on those hydrodynamics sub-layers, characteristic depths for concentrations can be deducted:
-
outter diffusive sub-layer: δOD corresponds to the “characteristic lengthscale of diffusion resulting from the blocking of large eddies” [24]. It was found by Magnaudet and Calmet [28] that the RMS of concentration fluctuations reaches its maximum value at z = δOD;
-
batchelor sub-layer: In this region, mass transfer is assumed purely diffusive, providing that even the smallest eddies should not be able to impact it.
One of the aim of the following work will be precisely to check for the existence of these conceptual sub-layers and to see in which way they influence mass transfer. A better insight into characteristic turbulent structures should be given by the use of a three-component velocimetry technique presented in Section 2.2.
2 Experimental Setup
2.1 Oscillating Grid Turbulence
Oscillating Grid Turbulence (OGT) is a mean of producing turbulence in a liquid initially at rest, by making a grid oscillate at a given frequency and a given amplitude. The periodic jets and wakes generated by the grid displacement interact and generate turbulence, which then diffuses away from the grid.
This principle was first designed in a goal of creating homogeneous and isotropic turbulence with zero mean flow [29]. Studies have yet shown that turbulence in such tanks is not fully homogeneous and isotropic [30] and that more or less strong mean flow still exist [31]. Anyway, the fact that turbulence characteristics can be well controlled by grid-oscillation parameters (as shown in what follows) and that the recirculation velocities remain at most of the same order of magnitude than the turbulence fluctuations, makes it an interesting device to study turbulence influence on dissolution at a gas liquid interface. Furthermore, this offers the advantage to set the interface’s location during all experimental trials whatever the used regime is.
For this study, the grid is placed in a prismatic tank of inner dimension 277-277-550 mm. The walls and the lid of the tank are made of transparent plexiglass to allow flow visualisation from various angles.
The grid has square section bars of side d = 7 mm and its mesh size is M = 35 mm so that its solidity is  which is below the maximum value of σmax = 0.4 recommended by Thompson and Turner [29] for optimal homogeneity of such turbulence. The motion of the grid is produced by a motor driving the motion of a crankshaft type system, the eccentricity of which being adjustable. This allows to vary the amplitude of the grid oscillations, or stroke, between S = 2.5 cm and S = 7.3 cm The frequency is set by the motor’s rotation speed and may vary between f = 0.1 Hz and f = 2 Hz.
which is below the maximum value of σmax = 0.4 recommended by Thompson and Turner [29] for optimal homogeneity of such turbulence. The motion of the grid is produced by a motor driving the motion of a crankshaft type system, the eccentricity of which being adjustable. This allows to vary the amplitude of the grid oscillations, or stroke, between S = 2.5 cm and S = 7.3 cm The frequency is set by the motor’s rotation speed and may vary between f = 0.1 Hz and f = 2 Hz.
It is possible to define a Reynolds number based on the grid parameters only, as it has been done by Janzen et al. [10]: (15)
(15)
The parameters chosen for this study are f = 1 Hz and S = 4.9 cm which corresponds to a grid Reynolds number of ReG = 2384.
Hopfinger and Toly [32] have established that the Root Mean Square (RMS) of horizontal and vertical velocity fluctuations u′ and v′ are only a function of the grid f, M, S and the distance zg to the average position of the grid such that: (16)where
(16)where  and
and  .
.
Moreover, Thompson and Turner [29] state that the integral length scale of turbulence depends linearly on zg: (17)where CTT ≃ 0.1.
(17)where CTT ≃ 0.1.
These relationships have been verified by a number of studies using grid stirred tanks [24, 25, 33-38] up to the values of the different constants which vary among the works (![$ {C}_{\mathrm{TT}}\in [0.1\dots 0.4],\enspace {\enspace C}_{{1}_{\mathrm{HT}}}\in [0.2\dots 0.3],\enspace {C}_{{2}_{\mathrm{HT}}}\in [1.1\dots 1.3]$](/articles/ogst/full_html/2017/01/ogst160138/ogst160138-eq38.gif) ). Validation of Hopfinger and Toly’s relationship (hereinafter called HT) have been made on the oscillating grid device used for this study and are presented in Section 3.
). Validation of Hopfinger and Toly’s relationship (hereinafter called HT) have been made on the oscillating grid device used for this study and are presented in Section 3.
When studying the influence of oscillating grid turbulence on an interface, the distance zg = H between this interface and the mean position of the grid is of great importance. As one can see from HT, velocity fluctuations’ intensity is an hyperbolic function of the distance to the grid, hence they tend to a zero asymptote far from the grid. Moreover, the horizontal homogeneity of turbulence is no longer ensured when too close to the grid, but typically reached at  with k = [2.5 … 4] depending on the study.
with k = [2.5 … 4] depending on the study.
For these reasons, the interface between the fluids should be positioned:
-
far enough from the interface, in order to free oneself from unwanted, non turbulent features and strong variations of turbulent intensity along the vertical direction;
-
close enough for the velocity fluctuations to be sufficiently energetic, and easily measurable.
The choice made here is to take  .
.
Based on this interface position, it is possible to compute the theoretical HT velocity scales based on HT relationships of Equation (16), and the undisturbed length-scale Linf, that is to say the integral length-scale of turbulence at zg = H if there were no interface. For the present configuration, it comes that L∞ = 24 mm,  and
and  .
.
Whith these turbulent scales, it can be checked using Chiapponi et al.’s experiments of surface fluctuations in grid stirred tanks [39], and Brocchini and Peregrine’s diagram of free surface deformation by liquid-side turbulence [40], that the shape of the interface remains in the “flat” domain.
At a given distance from the grid, it is possible to define a Reynolds number based on a velocity scale  predicted by HT relationships of Equation (16) for zg = H and on the undisturbed integral length scale L∞, as done by Brumley and Jirka [24]:
predicted by HT relationships of Equation (16) for zg = H and on the undisturbed integral length scale L∞, as done by Brumley and Jirka [24]: (18)with
(18)with 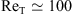 in these experiments.
in these experiments.
2.2 Velocity Field Measurements
Velocity fields are measured using a Stereoscopic Particle Image Velocimetry (SPIV) arrangement. In addition to the planar two dimensional velocity information given by traditional PIV measurements, SPIV also provides the third dimensional velocity component, and is therefore considered as a two dimensional three components velocimetry technique.The configuration chosen here is that of angular SPIV, in which the optical axis of each camera is shifted from the normal to the laser plane by an angle of α = 20° (Fig. 4). This value was found to be the best compromise between the maximum precision angle of 45° as stated by Prasad [41], and the camera adjustments. The principle of SPIV displacement measurement applied to a single particle is presented in Figure 5.
 |
Figure 5 Principle of SPIV measurements for a single particle. |
From a practical point of view, two hardships are inherent to SPIV measurements in liquid media:
-
depending on camera and lens’ adjustments, the depth of focus of each camera may not be sufficient to see distinctly the whole observation field from the SPIV slanted point of view. A solution to that problem is to shift the lens’ axis from the camera’s axis introducing a so called “Scheimpflug angle”. This misalignment distorts the depth of focus and adapts it to the measurement zone so that the full field becomes clear. The optimal Scheimpflug angle is found when the observation plane, the lens’ plane and the camera’s plane are colinear. This is the Scheimpflug condition detailed in Prasad’s state of art on SPIV techniques [41];
-
when using SPIV to measure liquid phase velocities, the inclination between camera’s axis and the normal to the tank’s walls leads to refraction phenomena at the wall and blurs the visualisation. To avoid refraction, the camera or lens’ axis has to be collinear with the normal to the wall. That is achieved by the addition of a liquid prism as explained in Prasad and Jensen [42].
For these experiments, the optimal Scheimpflug angle was found to be αS = 4°. The cameras used are double frame PCO CCD sensors of 1280 by 1024 pixels. A pulsed Quantel Nd:YAG laser emitting at λNd:YAG = 532 nm is used to illuminate Hollow Glass Spheres (HGS) particles of nominal diameter dparticles = 10 μm. The interval between two successive laser pulses is set at dtSPIV = 12 ms to optimise the displacement of particles in the 32 by 32 pixels interrogation windows. The spatial resolution of velocity field is 0.34 × 0.34 mm.
2.3 Concentration Field Measurement
The optical technique used to measure dissolved CO2 concentration fields is a variant of Planar Laser Induced Fluorescence (PLIF) methods that we call Blocked PLIF (BPLIF). Unlike what is done with traditional PLIF methods, the fluorescent dye is here previously homogeneously mixed into the liquid. Fluorescence of this dye under monochromatic light excitation is then inhibited (i.e. blocked) by the presence of a flow-passive scalar (temperature, viscosity, concentration of a chemical species, …). Thanks to a previous calibration operation, the observation of the fluorescence intensity map leads to the knowledge of the scalar value at any point of the recorded field.
In this study, fluorescein sodium (CAS number: 518-47-8) is used as a fluorescent tracer. When excited by an Argon-Ion monochromatic continuous laser emitting at λAr = 488 nm, it emits a fluorescence spectrum of wavelengths between λinf = 490 nm and λsup = 600 nm with an intense peak at λf = 515 nm. The pH dependency of its extinction coefficient ε and hence of its fluorescence intensity If (see Fig. 6), highlighted by Martin and Lindqvist [43] makes it a suitable dye to study [CO2] variations in water [44].
 |
Figure 6 Relative fluorescence intensity or extinction coefficient variations as a function of pH with data from Martin and Lindqvist [43], Walker [44] and the present study. |
The principle of BPLIF using fluorescein sodium as a fluorescent dye has been developed by Valiorgue et al. [1, 45] and is briefly summarized below.
It relies on the fact that after its dissolution into water, aqueous carbon dioxide interacts with water to form carbonic acid through the reaction (19)
(19)
Carbonic acid then dissociates into hydrogen carbonate  , and hydrogen carbonate into carbonate
, and hydrogen carbonate into carbonate  through the successive acid-base equilibria:
through the successive acid-base equilibria: (20)
(20)
A quantity often considered is the Dissolved Inorganic Carbon degree or DIC, which defines as![$$ \mathrm{DIC}=[\mathrm{C}{\mathrm{O}}_2{]}_{\mathrm{aq}}+[{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3]+[\mathrm{HC}{\mathrm{O}}_3^{-}]+[\mathrm{C}{\mathrm{O}}_3^{2-}] $$](/articles/ogst/full_html/2017/01/ogst160138/ogst160138-eq51.gif) (22)
(22)
As these reactions show, the presence of dissolved carbon dioxide somewhere inside the water locally produces H3O+ ions and as a result decreases the pH, leading to a local blocking of fluorescence intensity when the water is seeded with fluorescein.
The operations necessary to measure dissolved carbon dioxide fields are the following:
-
record fluorescence intensity field and apply correction taking into account non homogeneous excitation light intensity, and variations of extinction coefficient [45, 46];
-
convert intensity field to pH field using previously established calibration curves similar to the one shown in Figure 6;
-
convert pH field to [CO2]aq field using either theoretical solving of acid-base equilibria (Eqs. 19-21) as done in Figure 7, or an experimental [CO2]aq = f(pH) calibration curve previously established.

Figure 7 Numerical solution of chemical equilibria from Equations (19) to (21) for initially fixed pH of 7 and 10. Dashed lines are DIC concentrations and full lines aqueous CO2 concentrations. Horizontal lines show the equilibrium concentration for water under atmospheric partial pressure and 1 atm total pressure of gaseous carbon dioxide.
It can be checked that the intensity of fluorescence responds linearly to other factors such as laser intensity, concentration of dye or temperature [44].
For the following measurements, room temperature is fixed at Tair = 20 °C and a thermometer is used to check that water temperature is also Tw = 20 °C before and just after the experiment. The Continuous-Wave (CW) laser power is set at P = 1 W. Fluorescein concentration is chosen to be Cf = 5 × 10−7 based on Valiorgue’s experiments [1] and calibrations and trials are done sufficiently rapidly to avoid any time intensity variations.
Fluorescence fields are recorded by a LaVision sCMOS camera equiped with a 120 mm focal length lens. The sensor is a 2560 by 2160 pixels grid. PLIF techniques being spatially resolved up to the pixel size, this gives a spatial resolution for concentration fields of 0.008 × 0.008 mm.
The camera is used in its single frame configuration with an opening time of dtf = 10 ms, This time is chosen to be far greater than the time needed by dissolved CO2 to react and decrease the pH. This kinetic condition is a requirement for the technique’s ability to measure fluctuating concentration, as explained by Asher and Litchendorf [7].
Collecting light on a long opening time is also a way to ensure good signal over noise ratio and better precision for measurements. The limitation is that it has to be consequently lower than the fastest scalar transport time scale if one wants to be able to fix a recording rate fast enough to resolve scalar structures temporally. In this case two successive trials with two different lens aperture could be used to improve recorded intensity dynamical range [47]. Luckily, the scalar structures are relatively slow and its time scale range is estimated by Janzen et al. to be of about τscalar = [1−10] s for the considered turbulent velocity scales [10].
In order to use the full dynamics of the pH-intensity curve (Fig. 6), the pH of the water is initially fixed at pH0 = 10 by addition of sodium hydroxide (NaOH). With this initial condition, the fluorescence intensity of regions with zero dissolved CO2 concentration fluoresce at the higher intensity as possible, which increases the signal over noise ratio up to about 8 dB.
2.4 Coupling of Techniques
In order to study the influence of turbulence on scalar transport, it is of great interest to achieve simultaneous and spatially matched SPIV and BPLIF measurements.
2.4.1 Temporal Synchronisation
To ensure temporal synchronisation, the opening of both cameras are timed by a LaVision Programmable Time Unit (PTU), synchronised on the oscillating grid position if needed. The recording on the BPLIF image corresponds to the first SPIV laser pulse.
2.4.2 Laser Sheet
For coupled measurements, the Nd:YAG and Argon-Ion laser sheets have to be superimposed. This is achieved using a dichroic beam-splitter placed just after the two laser outputs as shown in Figure 4. Its cut-off wavelength of λc = 505 nm allows the λNd:YAG = 532 nm wavelength to go through whereas it reflects the λAr = 488 nm wavelength with yields up to 99% for 488 nm and 90% for 532 nm. The merged beams then go through the same optical arrangement details given in Figure 4.
2.4.3 Light Filtering
The BPLIF camera is equipped with a bandpass filter centred around λf1 = 515 nm so that the sensor collects only fluorescence signal and not Argon-Ion excitation light nor 532 nm light reflected on our HGS particles used as seeding for SPIV. In a similar way, low-pass filters of cut-off wavelength λf2 = 520 nm are placed in front of each SPIV camera to ensure that the fluorescence peak is not captured on their sensor and that the particle images remain bright enough with respect to the unwanted fluorescence background signal.
2.4.4 Spatial Resolution and Binning
As explained before, the spatial resolution of BPLIF technique is intrinsically better than SPIV or any PIV techniques providing that BPLIF is resolved up to the pixel size and SPIV up to the interrogation window’s size. With the aim of expressing turbulent correlation terms  as expressed in Section 1, it is necessary to spatially couple the information, hence reduce the scalar field resolution to that of the velocity field. This process is called binning. Two choices can be made as sketched in Figure 8:
as expressed in Section 1, it is necessary to spatially couple the information, hence reduce the scalar field resolution to that of the velocity field. This process is called binning. Two choices can be made as sketched in Figure 8:
-
pair each velocity vector with the scalar value at the center of the SPIV interrogation window projected on the scalar field, or an average on a N × N pixel square centred around this center, as in Variano and Cowen [12]. This may be called binning at center;
-
compute the average scalar value on each SPIV window projected on the scalar field and pair it with the corresponding vector. This would be called full binning.
 |
Figure 8 Binning options: a) no binning, b) full binning, c) binning at center. |
Binning at center is a faster processing technique but it needs the velocity field’s resolution to be high enough not to artificially sharpen scalar structures as in Figure 8. Full binning is slower but is physically closer to the principle of PIV algorithms where the velocity information is averaged over the interrogation window. It also tends to smooth local noise of scalar images. This is the option that has been selected here. For the used set-up, it is found that 32 by 32 pixels interrogation windows on SPIV cameras’ sensors correspond to 43 by 43 pixels squares on the BPLIF camera’s sensor.
3 Results and Discussion
3.1 Validation of the Grid Stirred Experiment
Validation of the grid stirred tank device used for this study has been made by Morge [48] using a classic PIV setup.
HT-type behaviour for RMS of velocity fluctuations is checked. The model constants are found to be C1HT = 0.27 and C2HT = 1.26. Figure 9 shows that the profiles move apart from HT model when approaching the interface and that the vertical velocity fluctuations become lower than the horizontal one in this region.
 |
Figure 9 Profiles of RMS of horizontal and vertical velocity components u′ and w′ and their prediction by Hopfinger and Toly’s relationships for f = 2 Hz, S = 2.9 cm i.e. ReG = 1670. |
It is checked that for the chosen H/M (see Sect. 2.1), an horizontally quasi homogeneous turbulent region of 10 cm by 10 cm exist at the center of the tank. The region of interest should therefore be included inside this homogeneity region.
A series of measurements synchronised with the grid’s position, as what is done by Escudié and Liné with a Rushton turbine impeller blade [49] are performed. This allows to account for oscillatory fluctuations induced by the grid’s motion. These measurements show no harmonic/oscillatory tendency on any of the velocity components, and the phased oscillating fluctuations are negligible with respect to the turbulent fluctuations in the region of interest. It is therefore assumed that velocity fluctuations at this distance of the grid are completely decorrelated from the stirring motion of the grid and are only due to turbulence.
3.2 Concentration Fields
3.2.1 Scalar Structures
BPLIF measurements are performed as explained in Section 2 for the grid stirring conditions presented before and with a gas phase composed of 100% of CO2 at atmospheric pressure. In these conditions, the theoretical saturation concentration is Csat = 1478.8 mg L−1. The initial bulk concentration is Cb0 = 0.5 mg L−1. The following results show the scaled concentration field  .
.
The recording of instantaneous concentration fields show several features:
-
a higly concentrated layer is visible just beneath the interface. Nonetheless, the estimation of it’s size based on instantaneous fields is not easy, due to the fact that it is constantly deformed by the fluid’s motion, and sometimes even totally swept (Fig. 10);

Figure 10 Instantaneous concentration fields. Red arrows show injection events and blue arrow renewal events.
-
Surface renewal and injections events can clearly be seen, and it appears that they are often coupled, as in Figure 10.
The apparent saturated concentration Csat is computed from a temporal average of concentration values of the 10 pixel lines just under the interface (corresponding to a 80 μm depth). It is found that Csat = 1.5 mg L−1 which is far from the theoretical saturation concentration value of Csat0 = 1478.8 mg L−1.
Several explanations are possible:
-
the purely diffusive layer in which the fluid is supposed to reach saturation concentration is in reality smaller that previous work’s observations (about 30-500 μm according to Herlina [16]). In these experiments, the theoretical Batchelor sub-layer as defined in Figure 3 is δB = 130 μm, which is supposed to be larger that the depth on which is averaged Csat. It should therefore be observable anyway;
-
pollution by PIV particles and laser reflections at the interface are non negligible and lead to an overestimation of fluorescence intensity, hence and underestimation of saturation concentration;
-
the hypothesis that a purely diffusive layer undisturbed by turbulence exists may be wrong. If so, renewal events may happen even directly at the interface, and this renewal may be too frequent for any the few sub-surface micrometers to have time to reach saturation. Such concentrations would therefore never be observable within the first instants of dissolutions as considered here.
Finally, complementary BPLIF trials in horizontal planes at different depth under the interface have been made by Morge [48]. The fluorescence intensity images from these measurements show clear scalar structures in horizontal planes, like in Figure 11.
 |
Figure 11 Horizontal fluorescence intensity recorded in a plane 5 mm under the interface by Morge [48]. |
This suggests that the velocity structures responsible for injections events are strongly three dimensional, and confirms the interest of SPIV application in this study.
3.2.2 Concentration Profile
Providing that the bulk concentration does not change significantly during a given recording time, it is possible to compute an image width averaged and time averaged concentration profile as a function of depth. An example of the computed profiles is drawn in Figure 12.
 |
Figure 12 Width and time averaged concentration profile and estimation of scalar characteristic depth δD. |
As a first approach, an estimate of the transfer velocity KL using a Lewis and Whitman type model, but taking turbulence into account can be derived from this profile. One may define the apparent concentration characteristic depth δD as the intersection between the tangent to the concentration profile at the interface, and the  vertical line, as in Figure 2. This depth scale takes into account for turbulent events, because the profile it is based on is itself averaged on a range of turbulent injections and renewal events.
vertical line, as in Figure 2. This depth scale takes into account for turbulent events, because the profile it is based on is itself averaged on a range of turbulent injections and renewal events.
Using this measured δD = 0.54 mm as the characteristic depth scale in Lewis and Whitman’s model (Eq. 7), it comes that  , which is coherent with mass transfer velocities found in grid stirred tank experiments of the literature for low grid Reynolds number [3].
, which is coherent with mass transfer velocities found in grid stirred tank experiments of the literature for low grid Reynolds number [3].
3.3 Velocity Fields
3.3.1 Instantanous Velocity Fields
The acquisition of three component velocity fields makes it possible to complete the classical planar observation of velocity structures with the out-of-plane velocity information. An example of SPIV acquired instantaneous velocity field is shown in Figure 13.
 |
Figure 13 Instantaneous velocity field in a vertical plane under the interface (black line): a) 2D projection and b) three component field. |
This velocity feature, clearly seen on the 2D view, proves to be highly three dimensional when looking at the three component field. One may especially notice an horizontal swirling along a slanted direction on almost all the measurement region, its intensity being higher at the interface.
This is precisely the type of structure that could be at the origin of horizontal scalar eddies as seen in Figure 11.
3.3.2 Statistics
As the measurement area is located within the surface-influenced layer, the vertical velocity fluctuation scale is, as expected, lower than that of horizontal velocities [10, 12].
The RMS of each velocity component is plotted on Figure 14 as a function of depth scaled by the viscous sub-layer’s size δv = 3.8 mm computed according to Brumley and Jirka. Each velocity component is scaled by its value at z = δv.
 |
Figure 14 RMS profiles of velocity fluctuations. z is scaled by the viscous sub-layer’s depth computed according to Brumley and Jirka. Velocities are scaled by their values at z = δv. |
The RMS profiles for the two horizontal velocity components appear to be very similar. In particular, they both show a maximum value at z = δv and superimposed for z < δv. This tendency would tend to confirm the existence of a statistically meaningful viscous sub-layer: even if some structures may be observed even inside this sub-layer, all velocity fluctuations components are globally decreasing in this region.
3.4 Simultaneous Measurements
The conditions for both BPLIF and SPIV measurements are reproduced and simultaneous measurements are recorded. This allows the visualisation of coupled scalar and velocity structures, as represented in Figure 15.
 |
Figure 15 Coupled concentration and velocity fields. a) Projected 2D view, b) 3D view. |
With this kind of synchronised measurement, it is easier to see the causal link between scalar structures and velocity patterns in the vertical plane. Injections events as of course associated with downward velocities and renewal events with upward velocities.
Moreover, three dimensional velocity fields confirm what was previously assumed: the planar scalar structures observed can also be explained by out-of-plane velocity component, as in Figure 15. For the injection event depicted by this figure, it is found that most of the high-concentration patch is brought downwards at the same time as the 3D structure visible on Figure 15b crosses the measurement area.
Conclusion and Perspectives
In this study an experimental set-up for the study of mass transfer was characterised and used to acquire simultaneous measurements of velocity and dissolved CO2 concentration in thin sub-layer under at a flat air water interface. A complex combination of injection and renewal events was observed on the instantaneous concentration fields. These events are explained by the corresponding instantaneous velocity field in an horizontal plane, but also by the third velocity component, which raises question about the impact of three dimensional velocity structures on mass transfer.
Such measurements are done to obtain quantitative results. In doing so we obtain statistical quantities such as mean velocity and concentration, the RMS of their fluctuations and ultimately their cross correlation, that is to say the turbulent mass flux for several independent samples.
The next interpretation step for coupled measurements will be an octant analysis of turbulent mass fluxes. Variano and Cowen [12] have already performed a quadrant analysis of mass transfer events in the vertical direction by sorting them into four categories according to the sign of w′ and c′. This allows them to quantify the relative impact of injection and renewal events, but not to determine the full characteristics of the mass flux in all direction. To account for horizontal transport that could be important to renewal processes, an octant sorting as proposed by Vinçont et al. [50] has to be considered, based on the signs of c′, w′ and u′.
A future objective of this study is to apply the same methodology to the analysis of mass transfer at an interface between a gas and a non-Newtonian fluid. In particular, studies have shown that the addition of a small quantity of polymer inside a Newtonian fluid tends to change significantly its hydrodynamic behaviour, especially in boundary layers, the most famous example being the drag reduction effect [51]. It would be therefore of great interest to study how these effects on hydrodynamics have an impact on mass transfer and dissolution phenomena at interfaces.
References
- Valiorgue P. (2012) Mass transfer in intermittent horizontal gas-liquid flow and application to photobioreactors, PhD Thesis, Université Claude Bernard Lyon I. [Google Scholar]
- Lewis W.K., Whitman W.G. (1924) Principles of gas absorption, Ind. Eng. Chem. 16, 12, 1215–1220. [Google Scholar]
- Turney D.E., Banerjee S. (2013) Air-water gas transfer and near-surface motions, J. Fluid Mech. 733, 588–624. [Google Scholar]
- Tsumori H., Sugihara Y. (2007) Lengthscales of motions that control air-water gas transfer in grid-stirred turbulence, J. Mar. Syst. 66, 1-4, 6–18. [Google Scholar]
- Herlina H., Jirka G.H. (2007) Turbulent gas flux measurements near the air-water interface in a grid-stirred tank, in Transport at the air-sea interface, environmental science and engineering, Garbe C.S., Handler R.A., Jähne B. (eds.), Springer, Berlin-Heidelberg, pp. 25–41. [Google Scholar]
- Variano E.A., Cowen E.A. (2007) Quantitative imaging of CO2 transfer at an unsheared free surface, in Transport at the air-sea interface, environmental science and engineering, Garbe C.S., Handler R.A., Jähne B. (eds.), Springer, Berlin-Heidelberg, pp. 43–57. [CrossRef] [Google Scholar]
- Asher W.E., Litchendorf T.M. (2008) Visualizing nearsurface concentration fluctuations using laser-induced fluorescence, Exp. Fluids 46, 2, 243–253. [Google Scholar]
- Herlina H., Jirka G.H. (2008) Experiments on gas transfer at the air-water interface induced by oscillating grid turbulence, J. Fluid Mech. 594, 183–208. [Google Scholar]
- Hasegawa Y., Kasagi N. (2009) Hybrid DNS/LES of high Schmidt number mass transfer across turbulent air-water interface, Int. J. Heat Mass Transfer 52, 3-4, 1012–1022. [CrossRef] [Google Scholar]
- Janzen J.G., Herlina H., Jirka G.H., Schulz H.E., Gulliver J.S. (2010) Estimation of mass transfer velocity based on measured turbulence parameters, AIChE J. 56, 8, 2005–2017. [Google Scholar]
- Kermani A., Khakpour H.R., Shen L., Igusa T. (2011) Statistics of surface renewal of passive scalars in free-surface turbulence, J. Fluid Mech. 678, 379–416. [Google Scholar]
- Variano E.A., Cowen E.A. (2013) Turbulent transport of a high-Schmidt-number scalar near an air-water interface, J. Fluid Mech. 731, 259–287. [Google Scholar]
- Herlina H., Wissink J.G. (2014) Direct numerical simulation of turbulent scalar transport across a flat surface, J. Fluid Mech. 744, 217–249. [Google Scholar]
- Simoens S. (1992) Application du traitement et de l’analyse d'images à des phénomenes de dispersion et de mélange turbulent, Thèse de Docteur de l’Ecole Centrale de Lyon, Lyon, France. [Google Scholar]
- Simoens S., Ayrault M. (1994) Concentration flux measurements of a scalar quantity in turbulent flows, Exp. Fluids 16, 3-4, 273–281. [Google Scholar]
- Herlina H. (2005) Gas transfer at the air-water interface in a turbulent flow environment, PhD Thesis, Universitätsverlag Karlsruhe, Karlsruhe. [Google Scholar]
- Higbie R. (1935) The rate of absorption of a pure gas into still liquid during short periods of exposure. AICHE Transactions, Vol. 37, p. 365–390. [Google Scholar]
- Danckwerts P.V. (1951) Significance of liquid-film coefficients in gas absorption, Ind. Eng. Chem. 43, 6, 1460–1467. [Google Scholar]
- Fortescue G.E., Pearson J.R.A. (1967) On gas absorption into a turbulent liquid, Chem. Eng. Sci. 22, 9, 1163–1176. [Google Scholar]
- Banerjee S., Scott D.S., Rhodes E. (1968) Mass transfer to falling wavy liquid films in turbulent flow, Ind. Eng. Chem. Fundam. 7, 1, 2227. [CrossRef] [Google Scholar]
- Lamont J.C., Scott D.S. (1970) An eddy cell model of mass transfer into the surface of a turbulent liquid, AIChE J. 16, 4, 513–519. [Google Scholar]
- Theofanous T.G. (1984) Conceptual models of gas exchange, in Gas transfer at water surfaces, number 2 in water science and technology library, Brutsaert W., Jirka G.H. (eds.), Springer, Netherlands, pp. 271–281. [CrossRef] [Google Scholar]
- McCready M.J., Vassiliadou E., Hanratty T.J. (1986) Computer simulation of turbulent mass transfer at a mobile interface, AIChE J. 32, 7, 1108–1115. [Google Scholar]
- Brumley B.H., Jirka G.H. (1987) Near-surface turbulence in a grid-stirred tank, J. Fluid Mech. 183, 235–263. [Google Scholar]
- Chu C.R., Jirka G.H. (1992) Turbulent gas flux measurements below the air-water interface of a grid-stirred tank, Int. J. Heat Mass Transfer 35, 8, 1957–1968. [CrossRef] [Google Scholar]
- Banerjee S., Lakehal D., Fulgosi M. (2004) Surface divergence models for scalar exchange between turbulent streams, Int. J. Multiphase Flow 30, 7-8, 963–977. [CrossRef] [Google Scholar]
- Hunt J.C.R., Graham J.M.R. (1978) Free-stream turbulence near plane boundaries, J. Fluid Mech. 84, 2, 209–235. [Google Scholar]
- Magnaudet J., Calmet I. (2006) Turbulent mass transfer through a flat shear-free surface, J. Fluid Mech. 553, 155–185. [Google Scholar]
- Thompson S.M., Turner J.S. (1975) Mixing across an interface due to turbulence generated by an oscillating grid, J. Fluid Mech. 67, 2, 349–368. [Google Scholar]
- De Silva I.P.D., Fernando H.J.S. (1994) Oscillating grids as a source of nearly isotropic turbulence, Phys. Fluids (1994-present) 6, 7, 2455–2464. [CrossRef] [Google Scholar]
- McKenna S.P., McGillis W.R. (2004) Observations of flow repeatability and secondary circulation in an oscillating grid-stirred tank, Phys. Fluids (1994-present) 16, 9, 3499–3502. [CrossRef] [Google Scholar]
- Hopfinger E.J., Toly J.-A. (1976) Spatially decaying turbulence and its relation to mixing across density interfaces, J. Fluid Mech. 78, 1, 155–175. [Google Scholar]
- Mcdougall T.J. (1979) Measurements of turbulence in a zero-mean-shear mixed layer, J. Fluid Mech. 94, 3, 409–431. [Google Scholar]
- Nokes R.I. (1988) On the entrainment rate across a density interface, J. Fluid Mech. 188, 185–204. [Google Scholar]
- De Silva I.P.D., Fernando H.J.S. (1992) Some aspects of mixing in a stratified turbulent patch, J. Fluid Mech. 240, 601–625. [Google Scholar]
- Xuequan E., Hopfinger E.J. (1986) On mixing across an interface in stably stratified fluid, J. Fluid Mech. 166, 227–244. [Google Scholar]
- Matsunaga N., Sugihara Y., Komatsu T., Masuda A. (1999) Quantitative properties of oscillating-grid turbulence in a homogeneous fluid, Fluid Dyn. Res. 25, 3, 147–165. [Google Scholar]
- Herlina H., Jirka G.H. (2004) Application of LIF to investigate gas transfer near the air-water interface in a grid-stirred tank, Exp. Fluids 37, 3, 341–349. [Google Scholar]
- Chiapponi L., Longo S., Tonelli M. (2012) Experimental study on oscillating grid turbulence and free surface fluctuation, Exp. Fluids 53, 5, 1515–1531. [Google Scholar]
- Brocchini M., Peregrine D.H. (2001) The dynamics of strong turbulence at free surfaces. Part 1. Description, J. Fluid Mech. 449, 225–254. [CrossRef] [MathSciNet] [Google Scholar]
- Prasad A.K. (2000) Stereoscopic particle image velocimetry, Exp. Fluids 29, 2, 103–116. [Google Scholar]
- Prasad A.K., Jensen K. (1995) Scheimpflug stereocamera for particle image velocimetry in liquid flows, Appl. Opt. 34, 30, 7092. [CrossRef] [PubMed] [Google Scholar]
- Martin M.M., Lindqvist L. (1975) The pH dependence of fluorescein fluorescence, J. Lumin. 10, 6, 381–390. [Google Scholar]
- Walker D.A. (1987) A fluorescence technique for measurement of concentration in mixing liquids, J. Phys. E: Sci. Instrum. 20, 2, 217. [CrossRef] [Google Scholar]
- Valiorgue P., Souzy N., El-Hajem M., Hadid H.B., Simoëns S. (2013) Concentration measurement in the wake of a free rising bubble using planar laser-induced fluorescence (PLIF) with a calibration taking into account fluorescence extinction variations, Exp. Fluids 54, 4, 1–10. [Google Scholar]
- Souzy N. (2014) Experimental study and improvement of mass transfer in vertical bubble columns, PhD Thesis, Université Claude Bernard Lyon I. [Google Scholar]
- Ayrault M., Simoens S. (1995) Turbulent concentration determination in gas flow using multiple CCD cameras, J. Flow Visualization Image Processing 2, 2, 195–208. [CrossRef] [Google Scholar]
- Morge F. (2015) Étude du transfert de masse gaz-liquide dans un écoulement stratifié, Rapport de Stage – Master 2 MEGA Spécialité Mécanique des Fluides, INSA de Lyon, Lyon, France. [Google Scholar]
- Escudié R., Liné A. (2003) Experimental analysis of hydrodynamics in a radially agitated tank, AIChE J. 49, 3, 585–603. [Google Scholar]
- Vinçont J.-Y., Simoëns S., Ayrault M., Wallace J.M. (2000) Passive scalar dispersion in a turbulent boundary layer from a line source at the wall and downstream of an obstacle, J. Fluid Mech. 424, 127–167. [Google Scholar]
- Lumley J.L. (1969) Drag reduction by additives, Annu. Rev. Fluid Mech. 1, 1, 367–384. [Google Scholar]
Cite this article as: T. Lacassagne, M. El-Hajem, F. Morge, S. Simoens and J.-Y. Champagne (2017). Study of Gas Liquid Mass Transfer in a Grid Stirred Tank, Oil Gas Sci. Technol 72, 7.
All Figures
 |
Figure 1 Principle of the experimental study. |
| In the text | |
 |
Figure 2 Diagram of liquid and gas concentration films adapted from Herlina [16]. |
| In the text | |
 |
Figure 3 Characteristics sub-layers according to Brumley and Jirka [24] extracted from Herlina [16]. η is the Kolmogorov length-scale of turbulence, Sc the Schmidt number, and L∞ and ReT the integral length-scale and Reynolds number defined in Section 2.1. |
| In the text | |
 |
Figure 4 Experimental set-up: a) side view, b) top view. |
| In the text | |
 |
Figure 5 Principle of SPIV measurements for a single particle. |
| In the text | |
 |
Figure 6 Relative fluorescence intensity or extinction coefficient variations as a function of pH with data from Martin and Lindqvist [43], Walker [44] and the present study. |
| In the text | |
 |
Figure 7 Numerical solution of chemical equilibria from Equations (19) to (21) for initially fixed pH of 7 and 10. Dashed lines are DIC concentrations and full lines aqueous CO2 concentrations. Horizontal lines show the equilibrium concentration for water under atmospheric partial pressure and 1 atm total pressure of gaseous carbon dioxide. |
| In the text | |
 |
Figure 8 Binning options: a) no binning, b) full binning, c) binning at center. |
| In the text | |
 |
Figure 9 Profiles of RMS of horizontal and vertical velocity components u′ and w′ and their prediction by Hopfinger and Toly’s relationships for f = 2 Hz, S = 2.9 cm i.e. ReG = 1670. |
| In the text | |
 |
Figure 10 Instantaneous concentration fields. Red arrows show injection events and blue arrow renewal events. |
| In the text | |
 |
Figure 11 Horizontal fluorescence intensity recorded in a plane 5 mm under the interface by Morge [48]. |
| In the text | |
 |
Figure 12 Width and time averaged concentration profile and estimation of scalar characteristic depth δD. |
| In the text | |
 |
Figure 13 Instantaneous velocity field in a vertical plane under the interface (black line): a) 2D projection and b) three component field. |
| In the text | |
 |
Figure 14 RMS profiles of velocity fluctuations. z is scaled by the viscous sub-layer’s depth computed according to Brumley and Jirka. Velocities are scaled by their values at z = δv. |
| In the text | |
 |
Figure 15 Coupled concentration and velocity fields. a) Projected 2D view, b) 3D view. |
| In the text | |





