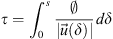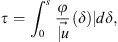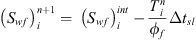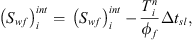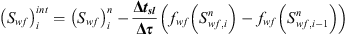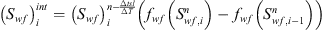Erratum to: Streamline simulation of water-oil displacement in a heterogeneous fractured reservoir using different transfer functions

Mohammad Mesbah; Ali Vatani; Majid Siavashi

doi:10.2516/ogst/2018068

Open Access

Erratum

This article is an erratum for:
[https://doi.org/10.2516/ogst/2018004]

Issue		Oil & Gas Science and Technology - Rev. IFP Energies nouvelles Volume 73, 2018


Article Number		81
Number of page(s)		1
DOI		https://doi.org/10.2516/ogst/2018068
Published online		18 December 2018

Oil & Gas Science and Technology - Rev. IFP Energies nouvelles 73, 81 (2018)

Erratum

Erratum to: Streamline simulation of water-oil displacement in a heterogeneous fractured reservoir using different transfer functions

Mohammad Mesbah¹, Ali Vatani² and Majid Siavashi³

¹ PhD Candidate of Petroleum Engineering, School of Chemical Engineering, Institute of Petroleum Engineering, University of Tehran, Tehran, Iran
² Professor of Chemical Engineering, Institute of LNG, College of Chemical Engineering, University of Tehran, Tehran Iran
³ Assistant Professor of Mechanical Engineering, Applied Multi-Phase Fluid Dynamics Laboratory, School of Mechanical Engineering, Iran University of Science and Technology, Tehran Iran

Accepted: 29 June 2018

Erratum for: Oil & Gas Science and Technology - Revue d’IFP Energies nouvelles 73, 14 (2018)

Some errors occurred in the online version of paper OGST170196, one should read:

Equation 12:

Correct form: $τ = \int_{0}^{s} \frac{\emptyset}{| \vec{u} (δ) |} dδ$ $\tau ={\int }_0^s\frac{\varnothing }{\left|\vec{u}(\delta )\right|}{d\delta }$ (12)

Instead of wrong form: $τ = \int_{0}^{s} \frac{φ}{\vec{| u}} (δ) | dδ,$ $\tau ={\int }_0^s\frac{\phi }{\overrightarrow{|u}}(\delta )|{d\delta },$ (12)

Equation 20:

Correct form: ${(S_{wf})}_{i}^{n + 1} = {(S_{wf})}_{i}^{int} - \frac{T_{i}^{n}}{ϕ_{f}} ∆ t_{sl}$ ${\left({S}_{{wf}}\right)}_i^{n+1}=\enspace {\left({S}_{{wf}}\right)}_i^{{int}}-\frac{{T}_i^n}{{\phi }_f}\Delta {t}_{{sl}}$ (20)

Instead of wrong form: ${(S_{wf})}_{i}^{int} = {(S_{wf})}_{i}^{int} - \frac{T_{i}^{n}}{ϕ_{f}} ∆ t_{sl},$ ${\left({S}_{{wf}}\right)}_i^{{int}}=\enspace {\left({S}_{{wf}}\right)}_i^{{int}}-\frac{{T}_i^n}{{\phi }_f}\Delta {t}_{{sl}},$ (20)

Equation 22:

Correct form: ${(S_{wf})}_{i}^{int} = {(S_{wf})}_{i}^{n} - \frac{Δ t_{sl}}{Δ τ} (f_{wf} (S_{wf, i}^{n}) - f_{wf} (S_{wf, i - 1}^{n}))$ ${\left({S}_{{wf}}\right)}_i^{{int}}={\left({S}_{{wf}}\right)}_i^n-\frac{\mathbf{\Delta }{{t}}_{{sl}}}{\mathbf{\Delta }{\tau }}\left({f}_{{wf}}\left({S}_{{wf},i}^n\right)-{f}_{{wf}}\left({S}_{{wf},i-1}^n\right)\right)$ (22)

Instead of wrong form: ${(S_{wf})}_{i}^{int} = {(S_{wf})}_{i}^{n - \frac{Δ tsl}{Δ T}} (f_{wf} (S_{wf, i}^{n}) - f_{wf} (S_{wf, i - 1}^{n}))$ ${\left({S}_{{wf}}\right)}_i^{{int}}={\left({S}_{{wf}}\right)}_i^{n-\frac{\Delta {tsl}}{\Delta T}}\left({f}_{{wf}}\left({S}_{{wf},i}^n\right)-{f}_{{wf}}\left({S}_{{wf},i-1}^n\right)\right)$ (22)

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.